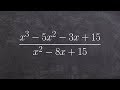
Rational Expressions and Factoring Techniques
Interactive Video
•
Mathematics
•
9th - 12th Grade
•
Practice Problem
•
Hard
Standards-aligned
Aiden Montgomery
FREE Resource
Standards-aligned
Read more
10 questions
Show all answers
1.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
Why can't properties of exponents be applied directly to simplify trigonometric expressions?
Because they are separated by addition and subtraction.
Because they involve complex numbers.
Because they are already in simplest form.
Because they are not polynomial expressions.
2.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the first step in factoring a trinomial?
Finding two numbers that multiply to the constant term and add to the middle coefficient.
Applying the quadratic formula.
Dividing the entire expression by the greatest common factor.
Rewriting the expression as a product of binomials.
3.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the grouping technique used for?
Finding the roots of a polynomial.
Simplifying rational expressions.
Solving quadratic equations.
Factoring expressions with four terms.
4.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
When using the grouping technique, what should you do after breaking the expression into two parts?
Divide the two parts by a common factor.
Multiply the two parts.
Add the two parts together.
Factor out the greatest common factor from each part.
5.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the common factor in the expression x^3 - 5x^2 - 3x + 15 after applying the grouping technique?
x + 5
x - 5
x + 3
x^2 - 3
6.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the importance of ensuring the same factors are factored out in the grouping technique?
To eliminate all terms in the expression.
To ensure a common factor can be factored out again.
To convert the expression into a quadratic.
To simplify the expression to a single term.
7.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the final simplified form of the expression after factoring by grouping?
(x - 3)(x^2 + 5)
(x + 3)(x^2 - 5)
(x + 5)(x^2 + 3)
(x - 5)(x^2 - 3)
Tags
CCSS.HSA.APR.D.6
Create a free account and access millions of resources
Create resources
Host any resource
Get auto-graded reports

Continue with Google

Continue with Email

Continue with Classlink

Continue with Clever
or continue with

Microsoft
%20(1).png)
Apple
Others
Already have an account?
Popular Resources on Wayground

10 questions
Forest Self-Management
Lesson
•
1st - 5th Grade

25 questions
Multiplication Facts
Quiz
•
5th Grade

30 questions
Thanksgiving Trivia
Quiz
•
9th - 12th Grade

30 questions
Thanksgiving Trivia
Quiz
•
6th Grade

11 questions
Would You Rather - Thanksgiving
Lesson
•
KG - 12th Grade

48 questions
The Eagle Way
Quiz
•
6th Grade

10 questions
Identifying equations
Quiz
•
KG - University

10 questions
Thanksgiving
Lesson
•
5th - 7th Grade
Discover more resources for Mathematics

10 questions
Identifying equations
Quiz
•
KG - University

20 questions
Pythagorean Theorem and Their Converse
Quiz
•
8th - 9th Grade

20 questions
Is it a Function?
Quiz
•
8th - 9th Grade

18 questions
Scatterplot Associations
Quiz
•
7th - 9th Grade

26 questions
Intro to Exponential Functions
Quiz
•
9th Grade

8 questions
211 - Write Equation Given Two Points
Quiz
•
9th Grade

16 questions
Solving Systems Review
Quiz
•
9th Grade

18 questions
Triangle Similarity Review
Quiz
•
9th - 12th Grade