Exploring Piecewise Functions in Advanced Mathematics

What is a piecewise function?

• A function that is not a true function but a relation.

• A function that is defined by a single rule.

• A function that only applies to positive values of x.

• A function that is defined in pieces with different rules for different parts of the domain.

Tags

CCSS.HSF-IF.C.7B

Why are piecewise functions considered actual functions?

• Because they pass the horizontal line test.

• Because they are defined by a single equation.

• Because they pass the vertical line test.

• Because they can have multiple y-values for a single x-value.

Tags

CCSS.HSF-IF.C.7B

What is the main difference in the rules for different parts of the domain in a piecewise function?

• The rules are the same for all parts of the domain.

• Different parts of the domain follow different rules.

• The rules only apply to positive values of x.

• The rules only apply to negative values of x.

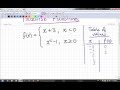
In the example given, what rule applies when x is less than 0?

• x^2 - 1

• x - 3

• x^2 + 1

• x + 3

Tags

CCSS.HSF.IF.A.2

What value of f(x) do you get when x = -2 in the given example?

• 0

• 3

• 1

• 2

Why is 0 not included in the domain for the rule x + 3?

• Because 0 is not a valid input for any function.

• Because 0 is included in the rule x^2 + 1.

• Because 0 is greater than 0.

• Because the rule x + 3 only applies to x less than 0.

Tags

CCSS.HSF.IF.A.2

What is the value of f(x) when x = 0 in the given example?

• 0

• -1

• 1

• 2

Tags

CCSS.HSF.IF.A.2

What is the value of f(x) when x = 2 in the given example?

• 6

• 5

• 4

• 3

Tags

CCSS.HSF.IF.A.2

What is the value of f(x) when x = 3 in the given example?

• 7

• 8

• 9

• 6

Tags

CCSS.HSF-IF.C.7B

What does the graph of the given piecewise function look like?

• A single continuous line.

• Two separate lines with a gap at x = 0.

• A parabola.

• A circle.

Tags

CCSS.HSF-IF.C.7B