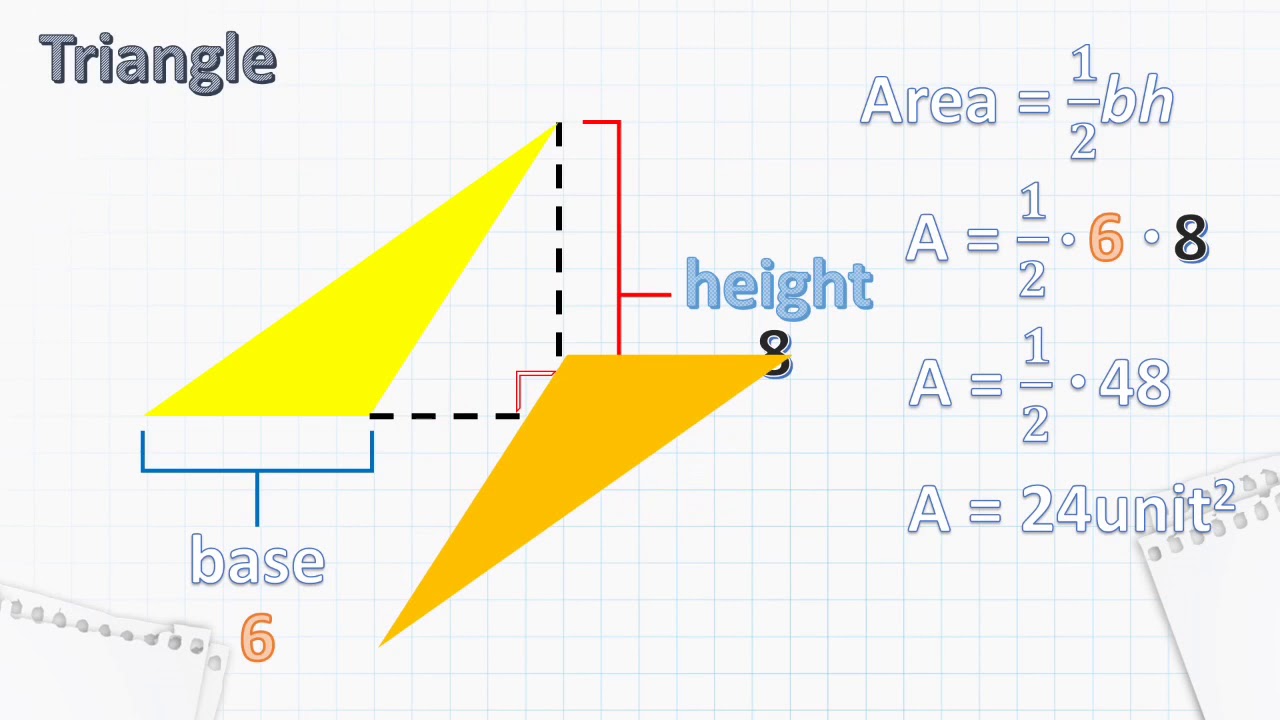
Calculating Areas of Geometric Shapes

This video tutorial covers area formulas for 2D geometric shapes: rectangles, parallelograms, triangles, and trapezoids. It explains not only how to calculate the area of these shapes but also why the formulas work. The video begins with a review of basic area concepts, then delves into each shape's specific formula, highlighting the importance of perpendicular heights and base measurements. The tutorial also demonstrates how each shape's area formula is derived from the rectangle's formula, emphasizing the mathematical reasoning behind these calculations.

What is the primary method taught in elementary school for calculating the area of a shape?

• Applying Pythagoras' theorem

• Using a ruler to measure the sides

• Counting the number of square units inside the shape

• Estimating visually

Why are square units used in area calculation?

• To measure the surface covered

• To measure perimeter

• To measure volume

• To measure density

What is the significance of right angles in calculating the area of polygons?

• They reduce the area

• They indicate the shape is a circle

• They are necessary for calculating volume

• They simplify the calculation

What is the formula for calculating the area of a rectangle?

• 2 x (Length + Width)

• Length / Width

• Length x Width

• Length + Width

How do you determine the height of a parallelogram for area calculation?

• It's the longest side of the parallelogram

• It's the length of any side

• It's the diagonal length

• It's perpendicular to the base

What does the 'height' in the parallelogram area formula refer to?

• The length of the slanted side

• The diagonal of the parallelogram

• The distance perpendicular to the base

• The length of the base

What makes a triangle's area formula different from a parallelogram's?

• It's double the parallelogram's formula

• It's exactly the same

• It involves the Pythagorean theorem

• It's half of the parallelogram's formula

How can the base of a triangle be identified for area calculation?

• Only the longest side can be the base

• Any side can be the base

• Only the shortest side can be the base

• It's always the bottom side

What is the area formula for a trapezoid?

• 1/2 x Height x (Base1 + Base2)

• Height x (Base1 - Base2)

• 1/2 x (Base1 x Base2) / Height

• Base1 x Base2 x Height

Why does the trapezoid area formula include '1/2' in its calculation?

• Because it's half of a parallelogram

• To double the area

• It's a mathematical error

• To adjust for the slanted sides