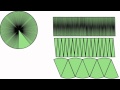
Exploring the Area of a Circle Formula

The video explains the derivation of the formula for the area of a circle, πr^2. It begins by visualizing the division of a circle into large parts and arranging them into a rectangle. As the circle is divided into smaller pieces, it resembles a rectangle more closely. The concept of infinite division is introduced to form a perfect rectangle. The video then calculates the dimensions of this rectangle, showing that the height is the radius and the base is half the circumference. Finally, it derives the formula πr^2 by combining these dimensions, demonstrating that the area of the circle equals the area of the rectangle.

What does πr^2 represent in geometry?

• Diameter of a circle

• Circumference of a circle

• Volume of a sphere

• Area of a circle

What shape does the circle start to resemble as it is divided into more parts?

• Triangle

• Square

• Rectangle

• Oval

What is the height of the rectangle formed by rearranging the circle's parts?

• Twice the radius of the circle

• Diameter of the circle

• Radius of the circle

• Circumference of the circle

How is the base of the rectangle determined when a circle is divided and rearranged?

• Equal to the circle's radius

• Half of the circle's circumference

• Twice the circle's radius

• Equal to the circle's diameter

Why do we divide the circle into smaller and smaller pieces?

• To make it easier to calculate

• To form a perfect rectangle

• To reduce the material used

• To increase the circle's area

What happens to the shape of the rearranged pieces as the circle is divided into smaller parts?

• It becomes less defined

• It becomes more circular

• It resembles a rectangle more closely

• It turns into a square

What mathematical operation combines the base and height to find the area of the rectangle?

• Multiplication

• Division

• Addition

• Subtraction

What is the relationship between the circle's circumference and the rectangle's base?

• The base is half the circumference

• There is no relationship

• The base is twice the circumference

• The base is the same as the circumference

How do we find the area of the circle using the rearranged rectangle?

• By subtracting the height from the base

• By dividing the base by the height

• By adding the base and height

• By multiplying the base by the height