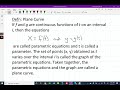
Understanding Parametric Equations Concepts

The video tutorial introduces parametric equations in a pre-calculus context, explaining their properties and how they differ from standard equations. It covers the concept of using time as a parameter and demonstrates how to graph these equations. The tutorial includes examples and applications, highlighting the flexibility of parametric equations in representing curves and paths in the x-y plane.

What is the shape of the graph for the equation y = 4 - (1/3)x^2?

• A circle

• An ellipse

• A hyperbola

• A parabola

In the context of parametric equations, what does the variable 'x' represent?

• The speed of an object

• A directed distance from the y-axis

• A directed distance from the x-axis

• The time parameter

What additional variable is introduced in parametric equations to describe the position of an object over time?

• Angle

• Distance

• Speed

• Parameter

If t = 0, what are the coordinates (x, y) for the parametric equations x = (3/2)t and y = 4 - (3/4)t^2?

• (0, 4)

• (3, 1)

• (3/2, 3)

• (0, 0)

What does the term 'orientation' refer to in the context of parametric equations?

• The distance between points on the graph

• The speed of the object

• The direction in which the curve is traced out as the parameter increases

• The shape of the graph

What is the effect of changing the parameter range on the graph of parametric equations?

• It changes the shape of the graph

• It changes the speed at which the graph is traced out

• It changes the color of the graph

• It changes the size of the graph

How can you find the inverse of a set of parametric equations?

• By integrating the equations

• By switching the x and y functions

• By solving for t

• By differentiating the equations

What is the shape of the graph for the parametric equations x = 2cos(θ) and y = 2sin(θ)?

• A circle

• A parabola

• A hyperbola

• An ellipse

Which of the following is NOT a characteristic of parametric equations?

• They can represent curves that are not functions

• They use a parameter to describe the position of points

• They always represent linear equations

• They can describe the motion of objects over time

What is the primary advantage of using parametric equations?

• They are always linear

• They are easier to solve

• They can represent more complex curves and motions

• They require fewer variables