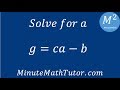
Solving for A in Equations

In this MinuteMath video, Sean Gann explains how to solve literal equations by isolating a specific variable. The example used is G = CA - B, which is solved for A. The process involves rewriting the equation, adding B to both sides, and dividing by C to isolate A. The final solution is A = (G + B) / C. The video concludes with a recap of the steps taken to reach the solution.

What is the initial equation given in the problem?

• G = C - A + B

• G = C + A - B

• G = CA - B

• G = A + B - C

Tags

CCSS.HSA.REI.A.1

What is the first step in solving the equation for A?

• Subtract B from both sides

• Multiply both sides by C

• Divide both sides by C

• Add B to both sides

Tags

CCSS.HSA.CED.A.4

After adding B to both sides, what does the equation become?

• G + B = CA

• G - B = CA

• G = A + B

• G = CA + B

Tags

CCSS.HSA.REI.A.1

What operation is used to isolate A after adding B to both sides?

• Multiplication

• Subtraction

• Division

• Addition

Tags

CCSS.HSA.REI.B.3

What is the purpose of dividing by C in the equation?

• To eliminate B

• To simplify the equation

• To isolate G

• To solve for A

Tags

CCSS.HSA.CED.A.4

What is the final expression for A?

• A = (G + B) * C

• A = C / (G + B)

• A = G + B / C

• A = G - B / C

Why is the equation rewritten with A first in the final expression?

• To eliminate variables

• To change the equation

• To make it look neat and organized

• To make it look more complex