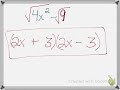
Factoring and Square Roots Concepts

This video tutorial explains how to factor expressions using the difference of two squares method. It covers the conditions for using this method, provides step-by-step examples, and explains the formula A^2 - B^2 = (A+B)(A-B). The tutorial emphasizes the importance of identifying perfect squares and using plus and minus signs to ensure the middle term cancels out.

What is the prerequisite for using the difference of two squares method?

• The terms must be prime numbers.

• The terms must be even numbers.

• The terms must be perfect squares and subtracted.

• The terms must be perfect cubes.

Tags

CCSS.HSA-REI.B.4B

In the first example, what is the square root of the first term, 4?

• 1

• 4

• 2

• 3

Tags

CCSS.HSA-REI.B.4B

What is the square root of the last term, 9, in the first example?

• 5

• 2

• 3

• 4

Tags

CCSS.8.EE.A.2

In the second example, what is the square root of 16?

• 5

• 2

• 3

• 4

Tags

CCSS.HSA-REI.B.4B

What is the square root of the first term, 9X^2, in the final example?

• 5X

• 3X

• 4X

• 2X

Tags

CCSS.HSA-REI.B.4B

What is the square root of the last term, 1, in the final example?

• 0

• 2

• 1

• 3

Why are plus and minus signs used in the factoring method?

• To simplify the expression.

• To add more terms to the expression.

• To make the expression more complex.

• To ensure the middle term is zero.

Tags

CCSS.HSA.APR.C.4

What is the formula for the difference of two squares?

• A^2 - B^2 = (A + B)(A - B)

• A^2 + B^2 = (A - B)(A + B)

• A^2 + B^2 = (A + B)(A - B)

• A^2 - B^2 = (A - B)(A - B)

Tags

CCSS.HSA.APR.C.4