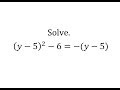
Solving Quadratic Equations and Solutions

The video tutorial explains how to solve a quadratic equation by using substitution. It begins by identifying the equation's quadratic form and introduces a substitution method to simplify it. The tutorial then demonstrates factoring the simplified equation and solving for the variable y. Finally, it verifies the solutions by substituting them back into the original equation to ensure they are correct.

What is the initial step in identifying the quadratic form of the given equation?

• Identifying the factors of y minus five

• Clearing the parentheses

• Factoring the equation

• Performing a substitution

Tags

CCSS.8.EE.C.7B

What substitution is made to simplify the equation?

• Let u equal y

• Let u equal y plus five

• Let u equal y squared

• Let u equal y minus five

Tags

CCSS.HSA-REI.B.4B

After substitution, what form does the equation take?

• u squared minus six equals negative u

• u squared plus six equals u

• u squared minus six equals u

• u squared plus six equals negative u

Tags

CCSS.HSA-REI.B.4B

What are the factors of the simplified equation u squared plus u minus six?

• (u + 2)(u - 3)

• (u - 2)(u + 3)

• (u + 1)(u - 6)

• (u - 1)(u + 6)

Tags

CCSS.HSA-REI.B.4B

How is the equation rewritten in terms of y after factoring?

• (y - 3)(y + 5)

• (y - 7)(y - 2)

• (y - 5)(y - 3)

• (y - 2)(y + 7)

Tags

CCSS.HSA-REI.B.4B

What are the solutions for y after solving the equation?

• y equals 5 or y equals 3

• y equals 4 or y equals 0

• y equals 7 or y equals 2

• y equals 6 or y equals 1

Tags

CCSS.8.EE.C.7B

What is the purpose of verifying the solutions?

• To simplify the equation further

• To find additional solutions

• To confirm the solutions satisfy the original equation

• To ensure the solutions are unique

Tags

CCSS.6.EE.B.5

What result confirms that y equals 2 is a solution?

• Negative two equals negative two

• Five equals five

• Three equals three

• Zero equals zero

Tags

CCSS.6.EE.B.5

What result confirms that y equals 7 is a solution?

• Five equals five

• Zero equals zero

• Three equals three

• Negative two equals negative two

Tags

CCSS.HSA-REI.B.4B

What is the final conclusion about the solutions?

• The solutions are incorrect

• The solutions are y equals 5 or y equals 3

• The solutions are y equals 7 or y equals 2

• The solutions are y equals 6 or y equals 1

Tags

CCSS.HSA-REI.B.4B