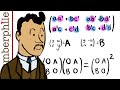
Matrix Factorizations and Their Applications

The video explores matrix factorizations, starting with basic polynomial factoring and extending to complex numbers. It highlights Dirac's use of matrices in quantum mechanics, explaining matrix multiplication and factorization. Eisenbud's theorem on matrix factorization is discussed, along with its applications and impact, including its use in string theory.

What is the main advantage of introducing complex numbers in polynomial factorization?

• They eliminate the need for real numbers.

• They allow for the factorization of polynomials that were previously unfactorable.

• They make calculations faster.

• They simplify the polynomial expressions.

How did complex numbers change the field of physics?

• They became fundamental in the development of quantum mechanics.

• They were used to simplify Newton's laws.

• They were used to develop new theories in classical mechanics.

• They replaced real numbers in all calculations.

What was Paul Dirac's innovative approach to solving the problem of finding a square root of a differential operator?

• Utilizing matrices to factor the operator.

• Ignoring the problem altogether.

• Applying classical mechanics principles.

• Using real numbers to approximate the solution.

What is a key property of matrix multiplication that differs from ordinary multiplication?

• Matrix multiplication is commutative.

• Matrices do not commute.

• Matrix multiplication is associative.

• Matrices always commute.

What was the significance of Dirac's use of matrices in quantum mechanics?

• It was only used in theoretical physics.

• It was a temporary solution with no lasting impact.

• It was quickly replaced by another method.

• It laid the foundation for matrix mechanics in quantum theory.

What is the main focus of Professor Eisenbud's most cited paper?

• The development of new polynomial equations.

• The history of complex numbers.

• The application of matrices in solving linear equations.

• The factorization of polynomials using matrices.

Why did Professor Eisenbud's paper gain significant attention in the field of string theory?

• It provided a new method for solving differential equations.

• It introduced a new type of matrix.

• It was the first paper to discuss string theory.

• It offered a theorem useful for defining boundary conditions in string theory.

What is a limitation of matrix factorization according to Professor Eisenbud?

• It cannot factor polynomials with more than three variables.

• It cannot factor polynomials with linear terms.

• It cannot factor polynomials with complex numbers.

• It cannot factor polynomials with constant terms.

What is the significance of excluding polynomials with constant or linear terms in matrix factorization?

• It ensures the factorization is non-trivial and informative.

• It simplifies the factorization process.

• It makes the factorization process faster.

• It allows for the use of real numbers only.

How did Professor Eisenbud's work impact the mathematical community?

• It provided a widely used theorem in various mathematical fields.

• It was largely ignored by mathematicians.

• It was only relevant to physicists.

• It introduced a new branch of mathematics.