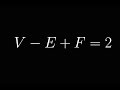
Understanding Euler's Formula and Graph Theory

The video explores Euler's characteristic formula, providing a unique proof using graph theory concepts like cycles, spanning trees, and dual graphs. It illustrates the concept of duality and its elegance in mathematics, explaining how planar graphs relate to Euler's formula. The video concludes with a proof showing the relationship between vertices, edges, and faces in a graph.

What is the main focus of the video tutorial?

• The theory of relativity

• The Pythagorean theorem

• Euler's characteristic formula

• Newton's laws of motion

Tags

CCSS.1.G.A.1

CCSS.2.G.A.1

In Euler's formula, what does 'V' stand for?

• Values

• Vectors

• Volumes

• Vertices

What is a cycle in graph theory?

• A path that starts and ends at the same vertex

• A graph with no edges

• A sequence of edges that never repeats

• A tree that spans all vertices

What is a spanning tree?

• A tree with multiple roots

• A connected graph without cycles that touches all vertices

• A disconnected graph with cycles

• A graph with cycles that spans all edges

What is the dual graph of a planar graph?

• A graph with no vertices

• A graph with the same number of vertices and edges

• A graph with twice the number of edges

• A graph where vertices are faces of the original graph

How are edges of the original graph related to the dual graph?

• They are unrelated to the dual graph

• They are half the number of edges in the dual graph

• They are the same as the edges of the dual graph

• They are twice the number of edges in the dual graph

What happens when Randolph buys all the edges of a spanning tree?

• Randolph creates a cycle in the graph

• Mortimer has no edges left to traverse

• Randolph disconnects the graph

• Mortimer is left with a spanning tree in the dual graph

What is the relationship between the number of vertices and edges in a tree?

• The number of edges is one more than the number of vertices

• The number of vertices is equal to the number of edges

• The number of edges is twice the number of vertices

• The number of vertices is one more than the number of edges

How does the dual graph help in proving Euler's formula?

• By illustrating that the number of vertices is twice the number of edges

• By demonstrating that the number of edges is equal to the number of faces

• By proving that the number of cycles equals the number of vertices

• By showing that the total number of edges is two more than the sum of vertices and faces

What is the significance of the dual graph in relation to the original graph?

• It halves the number of edges

• It disconnects the original graph

• It doubles the number of vertices

• It provides a symmetric relationship between cycles and connected components