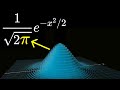
Understanding the Unreasonable Effectiveness of Mathematics
Interactive Video
•
Mathematics, Physics, Science
•
10th Grade - University
•
Hard
Sophia Harris
FREE Resource
Read more
10 questions
Show all answers
1.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the main theme of Eugene Wigner's paper discussed in the video?
The unreasonable effectiveness of mathematics in natural sciences
The complexity of mathematical equations
The role of technology in mathematics
The history of mathematics
2.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
In the anecdote, why was the classmate incredulous about the use of pi?
They thought pi was a fictional concept
They were unfamiliar with mathematical symbols
They believed pi was only used in geometry
They thought pi was irrelevant to population statistics
3.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the basic function that describes the bell curve shape in a Gaussian distribution?
e to the negative x squared
pi times x
x squared
e to the power of x
4.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
Why is pi significant in the formula for a normal distribution?
It represents the average value
It ensures the area under the curve is one
It is used to calculate the circumference
It is a placeholder for unknown values
5.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What mathematical tool is used to find the area under a curve?
Matrix
Vector
Integral
Derivative
6.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the purpose of introducing a higher-dimensional approach in the proof?
To simplify the calculations
To explore new mathematical concepts
To find the volume under a bell surface
To avoid using calculus
7.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What did John Herschel's derivation focus on?
The history of mathematics
The properties of radial symmetry and independence
The use of pi in geometry
The application of calculus in physics
Create a free account and access millions of resources
Create resources
Host any resource
Get auto-graded reports

Continue with Google

Continue with Email

Continue with Classlink

Continue with Clever
or continue with

Microsoft
%20(1).png)
Apple
Others
By signing up, you agree to our Terms of Service & Privacy Policy
Already have an account?
Popular Resources on Wayground

10 questions
Ice Breaker Trivia: Food from Around the World
Quiz
•
3rd - 12th Grade

20 questions
Halloween Trivia
Quiz
•
6th - 8th Grade

25 questions
Multiplication Facts
Quiz
•
5th Grade

4 questions
Activity set 10/24
Lesson
•
6th - 8th Grade

22 questions
Adding Integers
Quiz
•
6th Grade

10 questions
How to Email your Teacher
Quiz
•
Professional Development

15 questions
Order of Operations
Quiz
•
5th Grade

30 questions
October: Math Fluency: Multiply and Divide
Quiz
•
7th Grade
Discover more resources for Mathematics

20 questions
Translations, Reflections & Rotations
Quiz
•
8th - 10th Grade

14 questions
Model and Solve Linear Equations
Quiz
•
9th - 12th Grade

20 questions
SSS/SAS
Quiz
•
9th - 12th Grade

17 questions
Parallel lines cut by a transversal
Quiz
•
10th Grade

15 questions
Parallel and Perpendicular Lines
Quiz
•
9th - 10th Grade

20 questions
Corresponding Parts of Congruent Triangles
Quiz
•
10th Grade

12 questions
Slope Intercept Form Intro
Quiz
•
8th - 10th Grade

10 questions
Simplifying Expressions with the Distributive Property
Interactive video
•
6th - 10th Grade