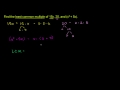
Understanding Least Common Multiple

The video tutorial explains how to find the least common multiple (LCM) of 15x, 20, and x^2 + 5x. It begins by breaking down numbers into their prime factors and expressions into their simplest components. The tutorial then demonstrates the prime factorization of 15x and 20, and the factoring of x^2 + 5x. It proceeds to construct the LCM by ensuring all necessary factors are included, and concludes by verifying the LCM through multiplication.

What is the first step in finding the least common multiple of numbers and expressions?

• Divide the numbers by each other.

• Multiply the numbers directly.

• Break them down into their smallest parts.

• Add the numbers together.

What is the prime factorization of 15?

• 2 * 7

• 3 * 5

• 5 * 5

• 2 * 3

How can 20 be expressed in terms of its prime factors?

• 4 * 5

• 2 * 10

• 3 * 5

• 2 * 2 * 5

What is the factored form of x^2 + 5x?

• x(x + 5)

• x^2 + 5

• x^2 - 5x

• x(x - 5)

Why is it necessary to include all factors when determining the LCM?

• To ensure the LCM is the smallest possible number.

• To make the calculation easier.

• To avoid using variables.

• To simplify the expression.

Which of the following is a necessary component for the LCM of 15x and 20?

• At least one 9

• At least one 2

• At least one 3

• At least one 7

What additional component is needed for the LCM to be divisible by x^2 + 5x?

• An additional 5

• An x + 5

• An x^2

• An additional 3

Tags

CCSS.8.EE.C.8B

CCSS.HSA.REI.C.6

What is the final expression for the least common multiple in this example?

• 60x(x + 5)

• 60(x + 5)

• 30(x + 5)

• 30x(x + 5)

Tags

CCSS.HSA.APR.A.1

What is the result of multiplying 60x by (x + 5)?

• 60x + 300

• 60x^2 + 5x

• 60x^2 + 300x

• 60x^2 + 60x

Tags

CCSS.7.EE.A.1

What is the purpose of distributing 60x in the final step?

• To factor the expression.

• To divide the expression.

• To simplify the expression.

• To add more variables.

Tags

CCSS.7.EE.A.1