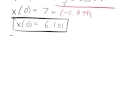
Fundamental Theorem of Calculus Applications

The video tutorial covers the fundamental theorem of calculus and its application in kinematics, particularly in finding position from velocity. It emphasizes the importance of this concept for AP and IB exams. The tutorial provides step-by-step problem-solving strategies and includes examples using both calculators and graphs to illustrate the application of the theorem.

What is the fundamental theorem of calculus primarily used for in the context of AP exams?

• To graph linear functions

• To calculate integrals and relate them to antiderivatives

• To find derivatives of functions

• To solve algebraic equations

How can the fundamental theorem of calculus be applied to kinematics?

• By solving for time using velocity

• By calculating the derivative of velocity

• By finding the position of an object using the integral of velocity

• By determining the acceleration from the position

When solving problems using the fundamental theorem of calculus, what is a common scenario?

• Using a calculator to find derivatives

• Graphing the original function

• Being given one value of the original function and asked for another

• Solving equations without a calculator

In the example problem involving a particle on the x-axis, why can't the integral be solved by hand?

• The integral is too simple

• The function is not continuous

• The function is not differentiable

• The integral is too complex to solve by hand

What is the initial position of the object if X(3) = 7 and the integral from 3 to 0 of V(t) dt is -0.899?

• 6.101

• 7.899

• 6.899

• 7.101

In the graph-based example, what is the significance of the area under the curve?

• It is irrelevant to the problem

• It shows the acceleration of the object

• It represents the velocity of the object

• It represents the change in position of the object

How is the area under the curve calculated in the graph-based example?

• By using the midpoint rule

• By estimating with a calculator

• By breaking it into geometric shapes

• By using the derivative of the function

What is the final position of the object if X(3) = 12 and the integral from 3 to 9 of the velocity function is 5?

• 17

• 12

• 5

• 7

Why is it important to consider the sign of the area under the curve in the graph-based example?

• It shows the maximum height reached

• It determines the time interval

• It affects the direction of the velocity

• It indicates whether the area is above or below the x-axis

What is a key takeaway from the video regarding the use of calculators in these problems?

• Calculators are used to check answers

• Calculators are essential for solving complex integrals

• Calculators are only used for graphing

• Calculators are not needed for any problems