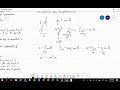
Pendulum Motion and Period Analysis

The video tutorial explains the derivation of the equation for the period of a pendulum. It begins with an introduction to the concept and the importance of understanding the equation's form. The tutorial then explores the forces acting on a pendulum, including weight and tension, and how these contribute to the restoring force. The relationship between displacement and acceleration in simple harmonic motion is discussed, leading to the derivation of the period equation. The final expression shows the period as a function of pendulum length and gravitational acceleration.

Why is understanding the derivation of the pendulum period equation important?

• It helps in understanding the equation's form.

• It is used in everyday calculations.

• It is a historical curiosity.

• It is required for exams.

What does the angle theta represent in the pendulum setup?

• The weight of the pendulum.

• The tension in the pendulum.

• The length of the pendulum.

• The angle of the pendulum's swing.

Which forces are considered when analyzing the pendulum's motion?

• Centripetal and centrifugal forces.

• Magnetic and electric forces.

• Weight and tension.

• Friction and air resistance.

What is the relationship between acceleration and net force in the context of the pendulum?

• Acceleration is equal to net force divided by mass.

• Acceleration is independent of net force.

• Acceleration is the inverse of net force.

• Acceleration is the square of net force.

In simple harmonic motion, how are acceleration and displacement related?

• They are directly proportional.

• They are inversely proportional.

• They are in opposite directions.

• They are unrelated.

What is the expression for angular frequency (omega) in terms of the period (T)?

• Omega equals T squared.

• Omega equals 2 pi over T.

• Omega equals T over 2 pi.

• Omega equals T times 2 pi.

How is the period (T) of a pendulum related to its length (L) and gravitational acceleration (G)?

• T is directly proportional to L and G.

• T is inversely proportional to L and G.

• T is proportional to the square root of L over G.

• T is proportional to the square of L over G.

What mathematical operation is used to simplify the final period equation?

• Square root

• Addition

• Multiplication

• Subtraction

What is the final form of the pendulum period equation?

• T = 4 pi squared times L over G

• T = 2 pi times the square root of G over L

• T = L over 4 pi squared times G

• T = 2 pi times the square root of L over G

Why is it important to be familiar with the pendulum period equation?

• It is rarely used in practical applications.

• It is a common exam question.

• It is used in advanced physics only.

• It is a fundamental concept in physics.