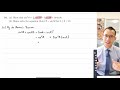
De Moivre's Theorem and Trigonometric Identities

The video tutorial explores the application of De Moivre's Theorem in solving complex trigonometric equations. The instructor explains how to identify when to use the theorem, particularly in problems involving integer multiples of angles. The tutorial demonstrates the expansion of complex numbers using binomial coefficients and focuses on separating real and imaginary parts to simplify the solution. The process of comparing imaginary parts and using the Pythagorean identity to eliminate cosine terms is also covered, leading to the final expression for sine 5 theta.

Why is De Moivre's Theorem particularly useful for solving trigonometric equations with large integer multiples of angles?

• It simplifies the process using binomial expansions.

• It directly provides the solution without calculations.

• It only works for angles less than 90 degrees.

• It eliminates the need for any trigonometric identities.

What is the first step in applying De Moivre's Theorem to a complex number?

• Separate the real and imaginary parts.

• Use the Pythagorean identity.

• Raise the complex number to the desired power.

• Convert the complex number to its rectangular form.

When expanding a complex number using De Moivre's Theorem, why is it helpful to separate real and imaginary parts?

• It is required by the theorem.

• It helps in comparing the parts later.

• It reduces the number of terms.

• It makes the calculation faster.

What role do binomial coefficients play in the expansion of a complex number using De Moivre's Theorem?

• They determine the number of terms in the expansion.

• They help in distributing powers between cosine and sine terms.

• They are used to calculate the power of the complex number.

• They are not used in this expansion.

Why is it necessary to eliminate cosine terms when comparing imaginary parts?

• Cosine terms are irrelevant in trigonometric equations.

• The original result does not contain cosine terms.

• Cosine terms complicate the calculations.

• Cosine terms are always zero.

Which identity is used to substitute cosine terms in the expansion?

• Euler's identity

• Pythagorean identity

• Trigonometric identity

• Complex number identity

What is the purpose of squaring both sides of the Pythagorean identity during substitution?

• To make the equation more complex.

• To simplify the equation further.

• To match the power of cosine terms.

• To eliminate sine terms.

What is the final result of expressing sine of 5 theta in terms of sine?

• It is expressed in terms of tangent.

• It is expressed purely in terms of cosine.

• It is expressed purely in terms of sine.

• It includes both sine and cosine terms.

How are like terms collected in the final simplification?

• By adding all terms together.

• By using a different identity.

• By grouping terms with the same power of sine.

• By eliminating all terms.

What indicates progress in solving the problem using De Moivre's Theorem?

• The use of a different theorem.

• The elimination of all terms.

• The expression of sine of 5 theta in terms of sine.

• The presence of cosine terms.