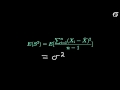
Understanding Sample Variance and Expectations

The video tutorial demonstrates that the sample variance is an unbiased estimator of the population variance. It explains why the sample variance formula divides by n-1 instead of n. The tutorial uses mathematical tools such as the expectation of a sum and the variance of a random variable. The proof involves calculating expectations and rearranging relationships to show that dividing by n-1 results in an unbiased estimator, while dividing by n would lead to a biased estimator.

What is the main goal of this video tutorial?

• To prove that sample variance is a biased estimator

• To explain the concept of standard deviation

• To demonstrate the calculation of mean

• To prove that sample variance is an unbiased estimator

Why do we divide by n-1 in the sample variance formula?

• To reduce the sample size

• To match the population variance

• To ensure the estimator is unbiased

• To make calculations easier

What is assumed about the observations X1 through Xn?

• They are dependent

• They have different means

• They are independent

• They have no variance

Which property of expectations is used in the proof?

• Expectation of a product is the product of expectations

• Expectation of a sum is the sum of expectations

• Expectation of a quotient is the quotient of expectations

• Expectation of a difference is the difference of expectations

What is the relationship between variance and expectation?

• Variance is the product of expectations

• Variance is the sum of expectations

• Variance is the expectation of the square minus the square of expectation

• Variance is the square of expectation

What is the expectation of the square of the sample mean?

• Mu squared

• Sigma squared times n

• Sigma squared divided by n plus mu squared

• Sigma squared

What is the first step in simplifying the expectation of the numerator?

• Multiplying by n

• Dividing by n

• Calculating the mean

• Ignoring the n-1

What happens when you square the sum of deviations?

• You get the sum of squares minus twice the product of mean and sum

• You get the sum of squares plus twice the product of mean and sum

• You get twice the sum of squares

• You get the sum of squares only

What is the final result of the proof regarding sample variance?

• Sample variance is an unbiased estimator

• Sample variance is always greater than population variance

• Sample variance is a biased estimator

• Sample variance equals population variance