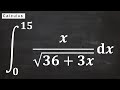
Definite Integrals and U-Substitution

This video tutorial covers the process of evaluating a definite integral using u-substitution. It begins with an introduction to definite integrals and the need for u-substitution due to the presence of a square root. The video then explains how to set up the u-substitution, simplify the integral, and perform the integration. After integrating, the tutorial demonstrates how to apply boundaries to the integrated function and evaluate the definite integral. The video concludes with a final evaluation and a reminder to keep learning.

What is the main topic introduced in the video?

• Indefinite Integrals

• Complex Numbers

• Definite Integrals

• Partial Derivatives

Why is evaluation necessary after integration in this context?

• To find the derivative

• Because of a logarithm

• Due to a square root sign

• To simplify the expression

What method is suggested to handle the square root in the integral?

• Integration by parts

• Partial fraction decomposition

• U-substitution

• Trigonometric substitution

What is the first step in performing a u-substitution?

• Find the derivative

• Set u equal to a part of the integrand

• Integrate directly

• Differentiate the entire expression

How is the integral transformed using u-substitution?

• By differentiating

• By using a trigonometric identity

• By integrating by parts

• By changing variables

Why is the integral split into two separate integrals?

• To simplify integration

• To apply the chain rule

• To use partial fractions

• To differentiate

What is done with constants during integration?

• They are integrated separately

• They are differentiated

• They are moved outside the integral

• They are ignored

What is added to the result after integration?

• A derivative

• A trigonometric function

• A constant of integration

• A logarithm

How are the boundaries changed after integration?

• They are doubled

• They are ignored

• They are converted to terms of u

• They remain the same

What is the final step in evaluating the definite integral?

• Simplifying the expression

• Adding more terms

• Differentiating the result

• Ignoring the boundaries