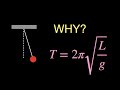
Pendulum Motion and Forces Concepts

The video tutorial explores the derivation of the pendulum period equation, starting with a GRE problem. It explains the forces acting on a pendulum and uses Newton's second law to derive the equation, employing a small angle approximation. The tutorial solves the differential equation and discusses the solution's implications for pendulum motion. It concludes with tips on memorizing and understanding the equation.

What is the main challenge in deriving the pendulum period formula during the GRE?

• The formula is too simple to remember

• The formula is not relevant to the exam

• The formula is not provided in the exam

• Lack of time to derive complex equations

Which forces act on a pendulum?

• Gravitational force and tension

• Magnetic force and tension

• Electrostatic force and gravitational force

• Friction and air resistance

What is the direction of the net force considered in the pendulum's motion?

• Along the arc length

• Perpendicular to the arc length

• Horizontally

• Vertically downward

How is the acceleration of the pendulum expressed in terms of angular displacement?

• Using the third derivative of angular displacement

• Using the first derivative of angular displacement

• Using the angular displacement itself

• Using the second derivative of angular displacement

What approximation is made for small angles in pendulum motion?

• The angle is approximately zero

• Sine of the angle is approximately equal to the angle

• Cosine of the angle is approximately equal to the angle

• Tangent of the angle is approximately equal to the angle

What is the relationship between angular frequency and the period of oscillation?

• Angular frequency is half the period

• Angular frequency is the reciprocal of the period

• Angular frequency is equal to the period

• Angular frequency is twice the period

Why is understanding derivations more beneficial than memorization?

• It is required for all exams

• It is easier to forget memorized formulas

• It takes less time than memorization

• It helps in reproducing the formula when needed