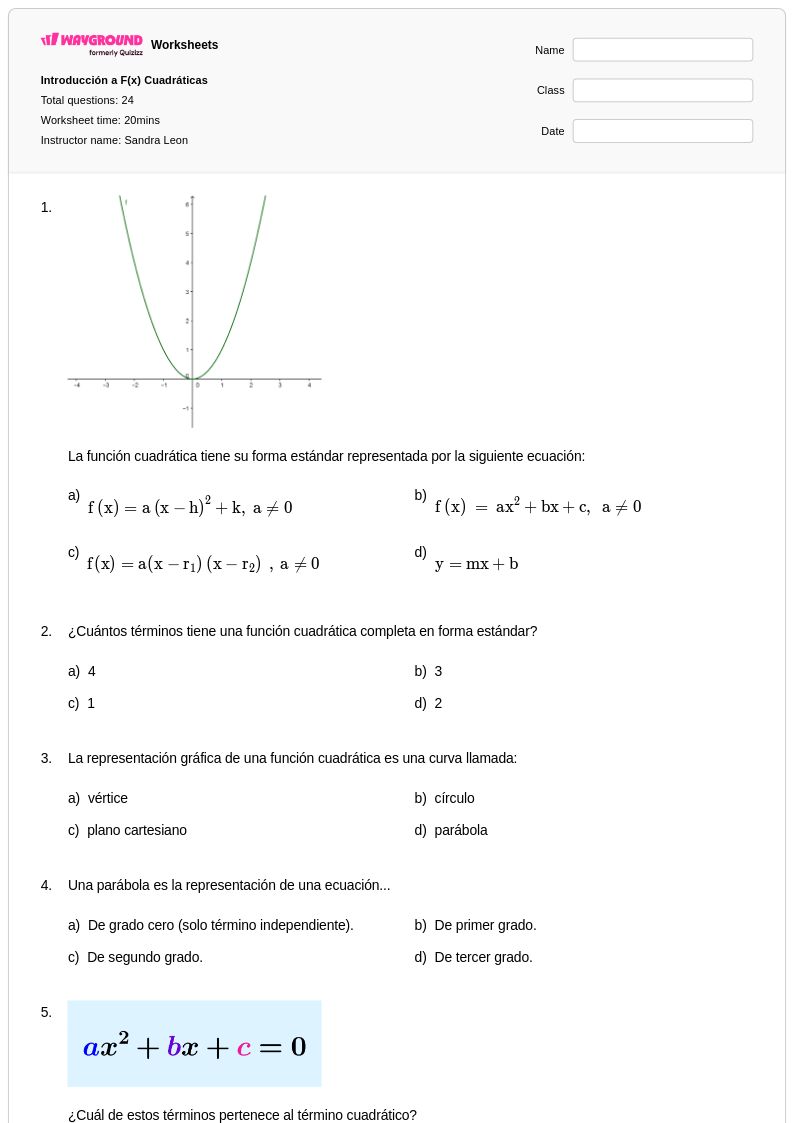
24Q
9th - 12th

22Q
9th - 12th
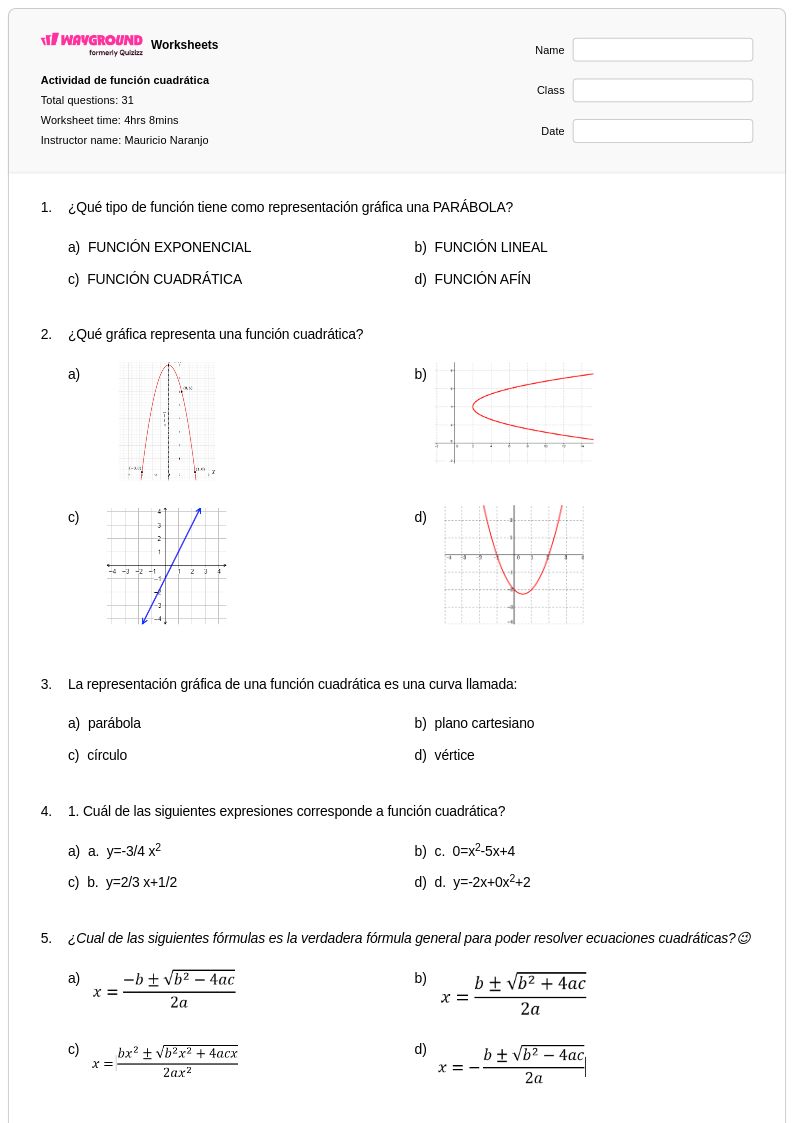
31Q
9th
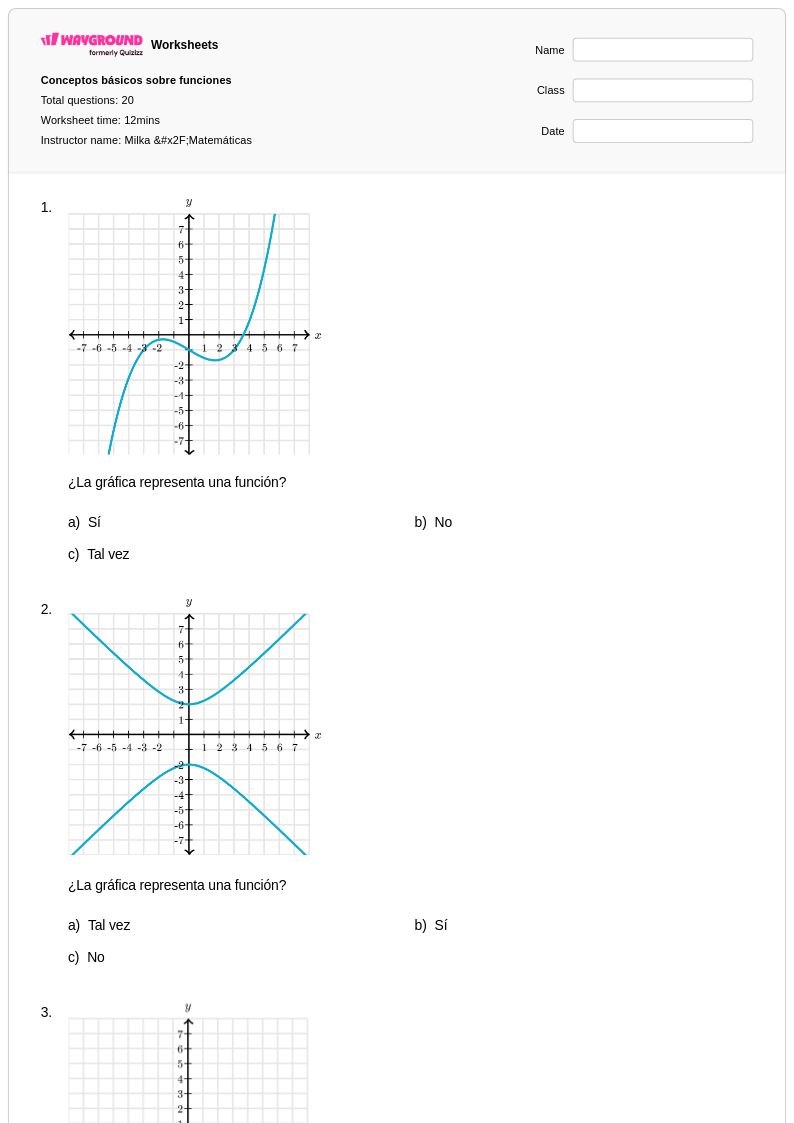
20Q
9th - 12th
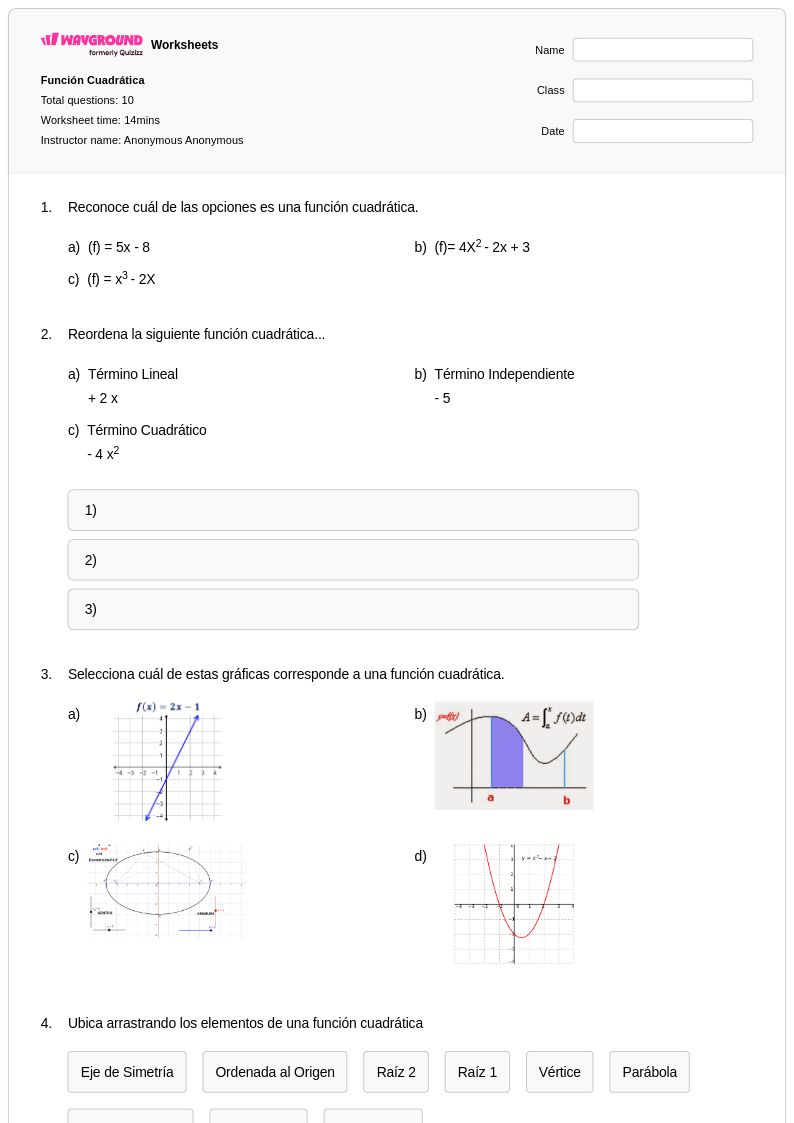
10Q
9th - 12th
20Q
9th - 12th

15Q
9th
20Q
9th
20Q
9th - 12th

20Q
1st - 12th
20Q
8th - 9th

15Q
9th - 12th
9Q
9th

20Q
9th

8Q
8th - 10th

10Q
9th
19Q
9th - Uni
11Q
9th - 12th

27Q
9th
10Q
9th

12Q
9th
10Q
1st - 10th

11Q
5th - Uni

12Q
9th - 12th
Explore otras hojas de trabajo de materias para grado 9
Explore las hojas de trabajo imprimibles de Partes de una parábola para Grado 9
Las hojas de trabajo sobre las partes de una parábola para estudiantes de 9.º grado ofrecen una práctica esencial para identificar y comprender los componentes fundamentales de las funciones cuadráticas y sus representaciones gráficas. Estas completas hojas de trabajo guían a los estudiantes en el reconocimiento de elementos clave, como el vértice, el eje de simetría, la intersección con el eje y, las intersecciones con el eje x (raíces o ceros), la dirección de apertura y el dominio y rango de las funciones parabólicas. Los estudiantes desarrollan habilidades analíticas críticas al resolver problemas que les exigen localizar estas partes tanto algebraica como gráficamente, sentando una base sólida para conceptos avanzados de funciones cuadráticas. La colección incluye claves de respuestas detalladas y recursos imprimibles gratuitos en formato PDF, lo que permite a los estudiantes verificar su comprensión y a los profesores evaluar eficazmente el dominio de estos conceptos algebraicos fundamentales.
Wayground, anteriormente Quizizz, ofrece a los educadores una extensa biblioteca de millones de recursos creados por docentes, diseñados específicamente para la enseñanza de las partes de una parábola en matemáticas de 9.º grado. Las robustas funciones de búsqueda y filtrado de la plataforma permiten a los docentes encontrar rápidamente hojas de trabajo que se ajustan a los estándares curriculares y se adaptan a las necesidades de aprendizaje específicas de sus estudiantes. Estos materiales versátiles están disponibles tanto en formato PDF imprimible como en versiones digitales, ofreciendo opciones flexibles de personalización que facilitan la enseñanza diferenciada para estudiantes diversos. Los docentes pueden integrarlos fácilmente en la planificación de clases, utilizarlos para la recuperación específica de estudiantes con dificultades, ofrecer oportunidades de enriquecimiento a estudiantes avanzados o asignarlos como práctica regular de habilidades para reforzar la comprensión conceptual de los componentes parabólicos en su currículo de álgebra.
