
8Q
1st - Uni
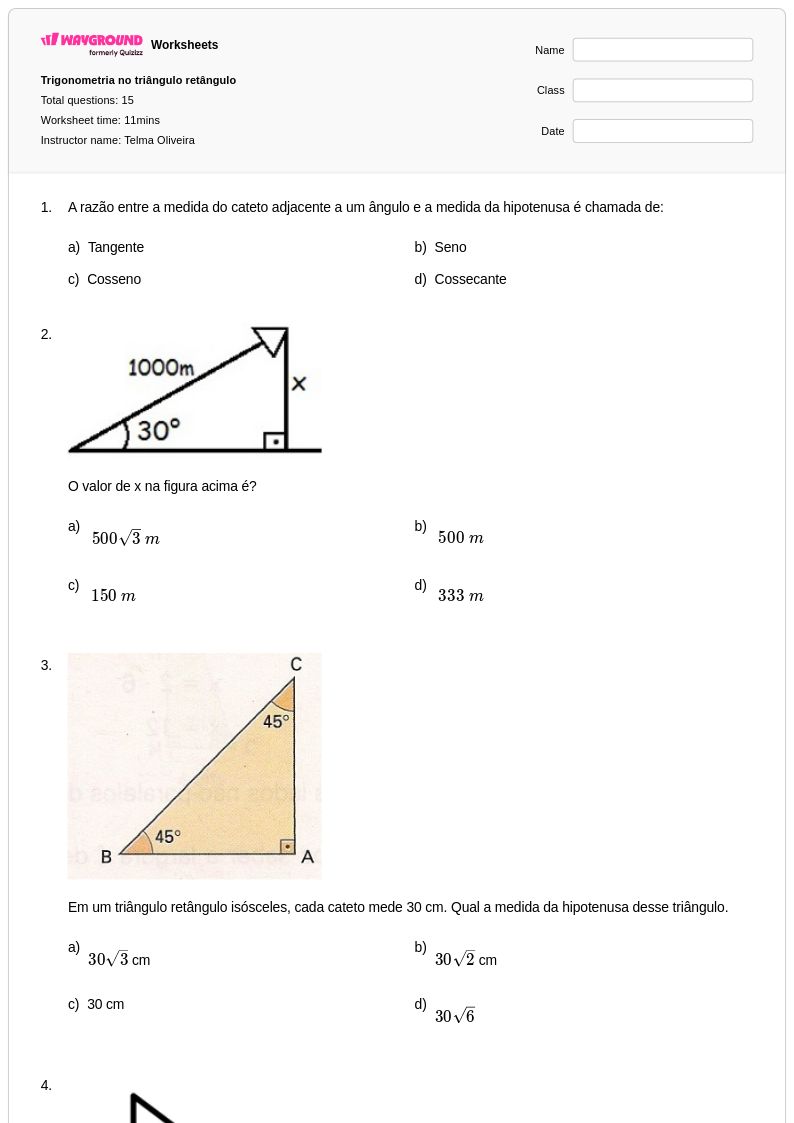
15Q
1st - 10th

9Q
6th

10Q
6th

8Q
6th

10Q
6th - 8th

8Q
6th

20Q
6th - 8th

11Q
6th
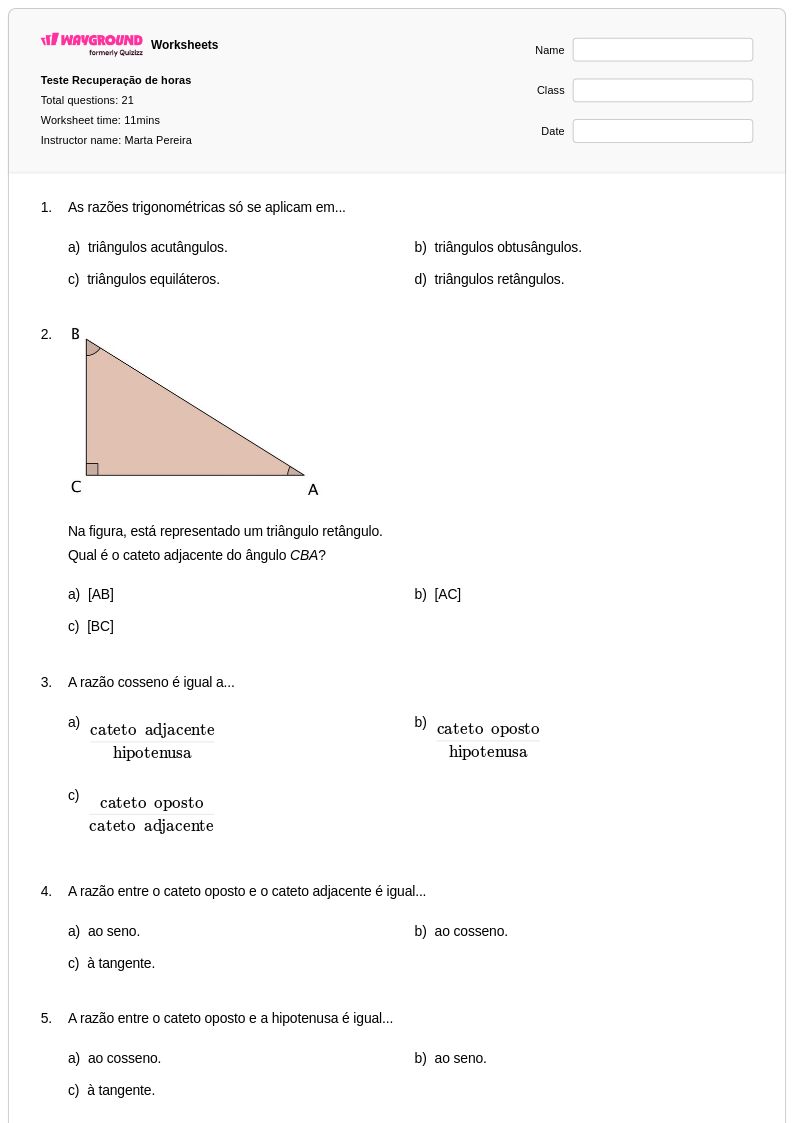
21Q
3rd - Uni

10Q
1st - Uni

12Q
6th

14Q
6th - 9th

18Q
5th - 8th

16Q
2nd - Uni

11Q
6th

15Q
6th

12Q
1st - 12th

24Q
6th

10Q
1st - 12th

29Q
6th
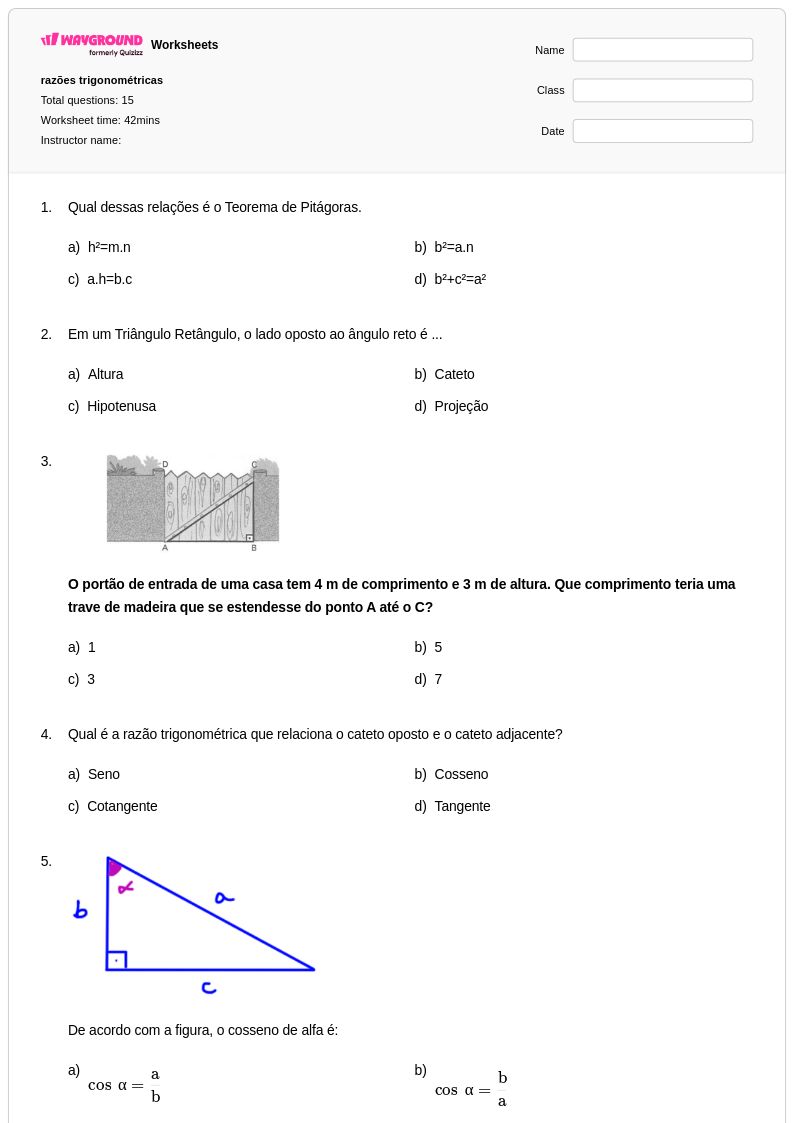
15Q
3rd - 11th

16Q
6th - 8th

12Q
6th
Explore planilhas Razões trigonométricas: seno, cosseno, tangente, cossecante, secante e cotangente. por notas
Explore outras planilhas de assuntos para série 6
Explore planilhas Razões trigonométricas: seno, cosseno, tangente, cossecante, secante e cotangente. imprimíveis para 6ª série
As razões trigonométricas, incluindo seno, cosseno, tangente, cossecante, secante e cotangente, formam a base fundamental para os alunos do 6º ano que estão iniciando sua jornada em conceitos matemáticos avançados. A coleção abrangente de exercícios de razões trigonométricas da Wayground oferece aos alunos problemas práticos estruturados que introduzem sistematicamente essas relações essenciais em triângulos retângulos. Esses recursos para impressão fortalecem a capacidade dos alunos de identificar os lados oposto, adjacente e hipotenusa, enquanto calculam valores trigonométricos básicos usando a notação matemática adequada. Cada exercício inclui um gabarito completo e está disponível para download gratuito em PDF, permitindo que os alunos resolvam os problemas em seu próprio ritmo, enquanto desenvolvem confiança na aplicação desses princípios matemáticos fundamentais que os servirão ao longo de suas trajetórias acadêmicas.
A extensa biblioteca da Wayground reúne milhões de recursos criados por professores, especificamente projetados para apoiar educadores no ensino eficaz de trigonometria para alunos do 6º ano. Os recursos robustos de busca e filtragem da plataforma permitem que os professores localizem rapidamente exercícios que estejam alinhados com os padrões curriculares específicos, oferecendo ferramentas de diferenciação para atender aos diferentes níveis de habilidade dos alunos na mesma sala de aula. Os professores podem personalizar esses materiais digitais e impressos para se concentrarem em razões trigonométricas específicas ou combinar vários conceitos para sessões de revisão abrangentes. Essa flexibilidade se mostra inestimável para o planejamento de aulas, reforço direcionado para alunos com dificuldades e oportunidades de enriquecimento para alunos avançados, garantindo que todos os alunos recebam a prática adequada para dominar essas relações matemáticas essenciais que conectam a geometria básica à trigonometria avançada.
