
14 คิว
6th - Uni

11 คิว
6th - Uni

11 คิว
6th - Uni
15 คิว
6th - 8th
28 คิว
6th - 8th

8 คิว
6th - 8th

40 คิว
6th - 8th

15 คิว
6th - Uni

11 คิว
6th - Uni

20 คิว
5th - Uni

20 คิว
6th - 8th

15 คิว
6th - Uni

20 คิว
6th - Uni
18 คิว
6th - Uni

20 คิว
6th - Uni

20 คิว
6th - Uni
20 คิว
6th - Uni
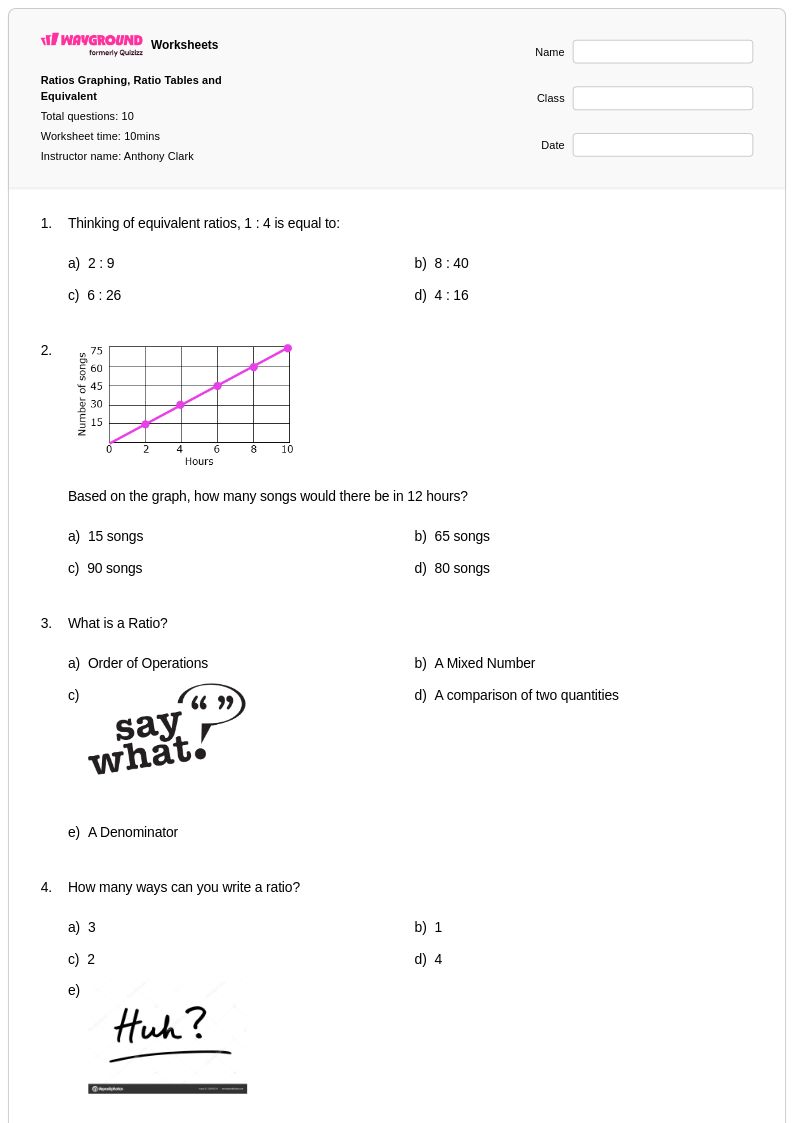
10 คิว
6th - Uni

15 คิว
6th - Uni

20 คิว
6th - Uni
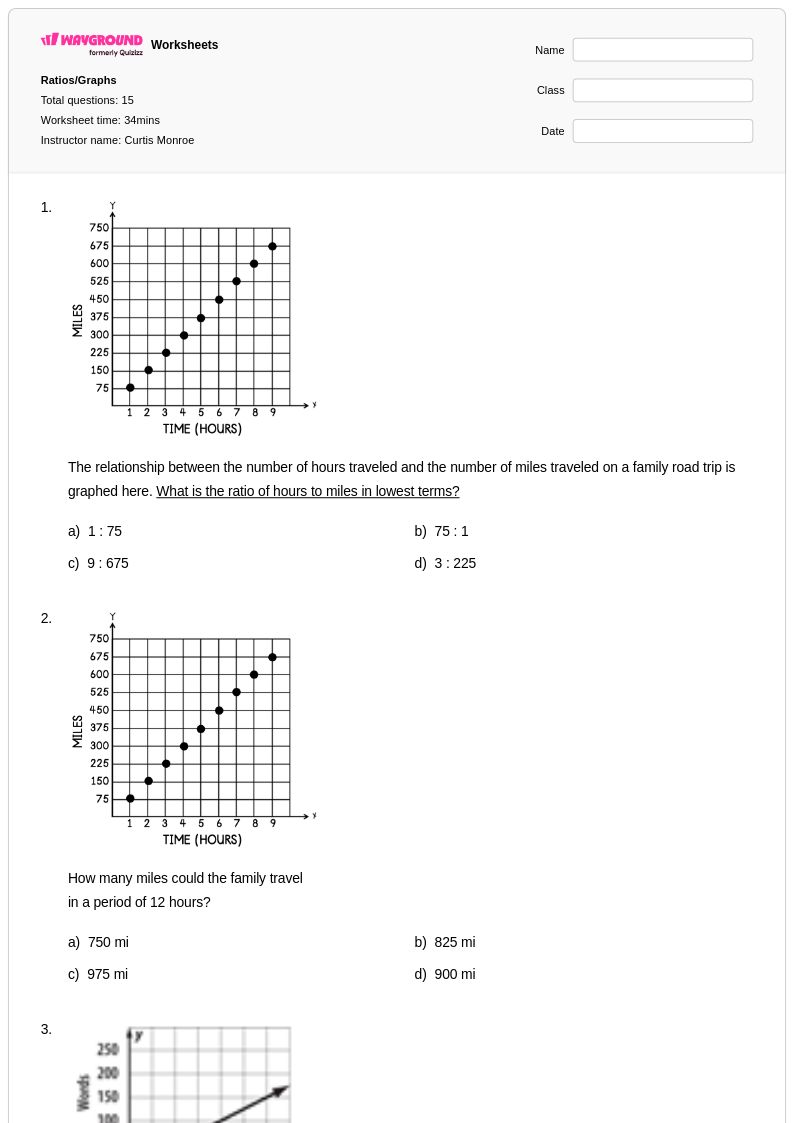
15 คิว
7th
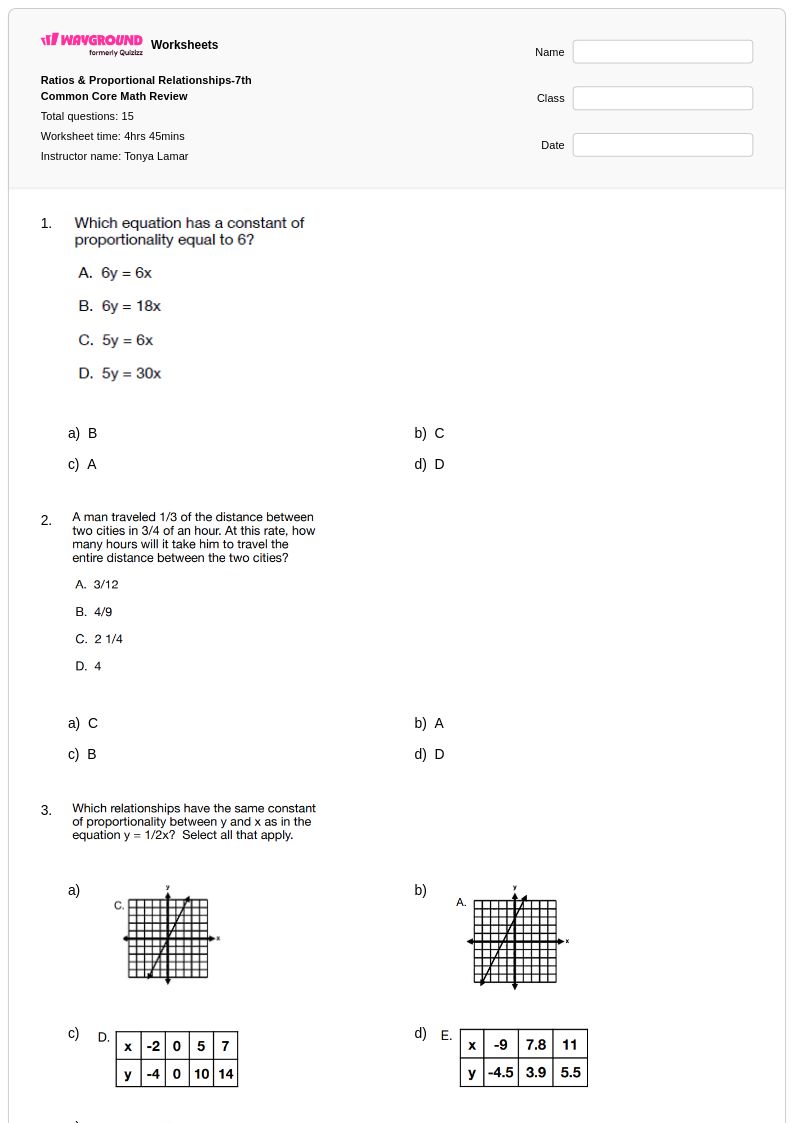
15 คิว
6th - 8th
11 คิว
6th - Uni
15 คิว
6th - Uni
สำรวจใบงานวิชาอื่นๆ สำหรับ ระดับ 7
สำรวจแผ่นงาน การสร้างกราฟอัตราส่วน ที่พิมพ์ได้สำหรับ ชั้นประถมศึกษาปีที่ 7
แบบฝึกหัดการวาดกราฟอัตราส่วนสำหรับนักเรียนชั้น ม.1 จาก Wayground (เดิมชื่อ Quizizz) ให้แบบฝึกหัดที่ครอบคลุมในการแสดงภาพความสัมพันธ์ตามสัดส่วนบนระนาบพิกัด แหล่งข้อมูลที่ออกแบบมาอย่างพิถีพิถันเหล่านี้ช่วยให้นักเรียนคณิตศาสตร์ชั้น ม.1 พัฒนาทักษะที่จำเป็นในการเขียนตารางอัตราส่วน การระบุรูปแบบในข้อมูลตามสัดส่วน และการตีความความหมายของจุดบนกราฟอัตราส่วน นักเรียนจะได้ทำแบบฝึกหัดที่ต้องแปลงตารางอัตราส่วนเป็นคู่พิกัด วาดกราฟความสัมพันธ์ตามสัดส่วน และวิเคราะห์รูปแบบเชิงเส้นที่เกิดขึ้น แบบฝึกหัดแต่ละชุดประกอบด้วยเฉลยคำตอบโดยละเอียดที่สนับสนุนการเรียนรู้ด้วยตนเองและการประเมินตนเอง ในขณะที่รูปแบบ PDF ที่พิมพ์ได้ฟรีช่วยให้เข้าถึงได้ทั้งสำหรับการเรียนการสอนในห้องเรียนและการบ้าน
Wayground (เดิมชื่อ Quizizz) ช่วยให้ครูผู้สอนมีคลังข้อมูลขนาดใหญ่ที่มีแบบฝึกหัดการวาดกราฟอัตราส่วนที่สร้างโดยครูผู้สอนนับล้านรายการ ซึ่งสอดคล้องกับมาตรฐานคณิตศาสตร์ชั้น ม.1 โดยเฉพาะ ความสามารถในการค้นหาและกรองข้อมูลที่แข็งแกร่งของแพลตฟอร์มช่วยให้ครูสามารถค้นหาแบบฝึกหัดที่ตรงกับข้อกำหนดหลักสูตรเฉพาะและระดับความสามารถของนักเรียนได้อย่างรวดเร็ว เครื่องมือปรับระดับความยากขั้นสูงช่วยให้ผู้สอนสามารถปรับระดับความยากของเนื้อหา แก้ไขความซับซ้อนของโจทย์ และปรับรูปแบบการนำเสนอภาพให้เหมาะสมกับความต้องการในการเรียนรู้ที่หลากหลาย ไม่ว่าครูจะต้องการแบบฝึกหัดในรูปแบบไฟล์ PDF สำหรับกิจกรรมในห้องเรียนแบบดั้งเดิม หรือรูปแบบดิจิทัลสำหรับบทเรียนแบบโต้ตอบ การส่งมอบทรัพยากรที่ยืดหยุ่นนี้สนับสนุนการวางแผนบทเรียนที่ราบรื่น การแก้ไขปัญหาอย่างตรงจุดสำหรับนักเรียนที่เรียนรู้ช้า และโอกาสในการเสริมสร้างทักษะสำหรับผู้เรียนที่มีความสามารถสูงที่ต้องการฝึกฝนทักษะเพิ่มเติมในการเขียนกราฟพิกัดและการให้เหตุผลเชิงสัดส่วน
