
7Q
9th - 12th

11Q
7th - 10th

7Q
9th - 12th

14Q
10th - Uni

15Q
9th - 12th

20Q
7th - Uni

10Q
9th - 12th
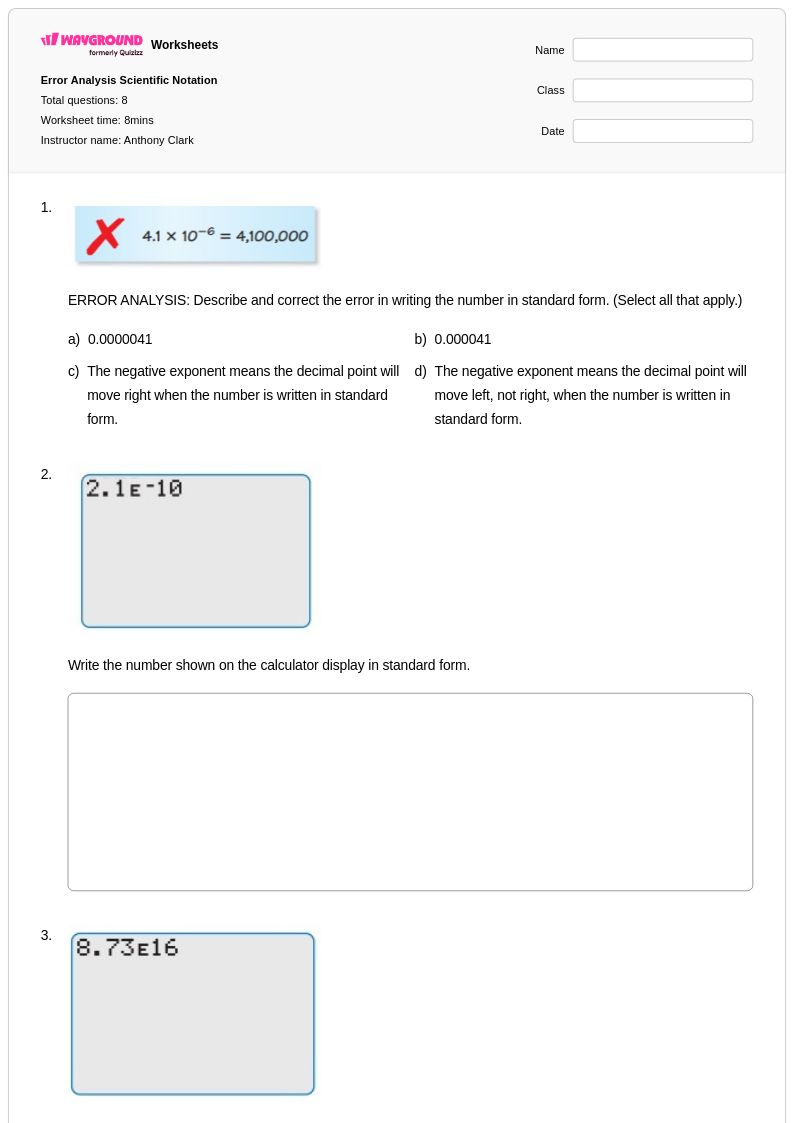
8Q
8th - Uni

11Q
10th

10Q
9th - Uni

20Q
9th - Uni

18Q
10th - Uni

10Q
9th - 10th

19Q
10th - Uni

17Q
9th - 12th

14Q
9th - 12th

10Q
9th - Uni
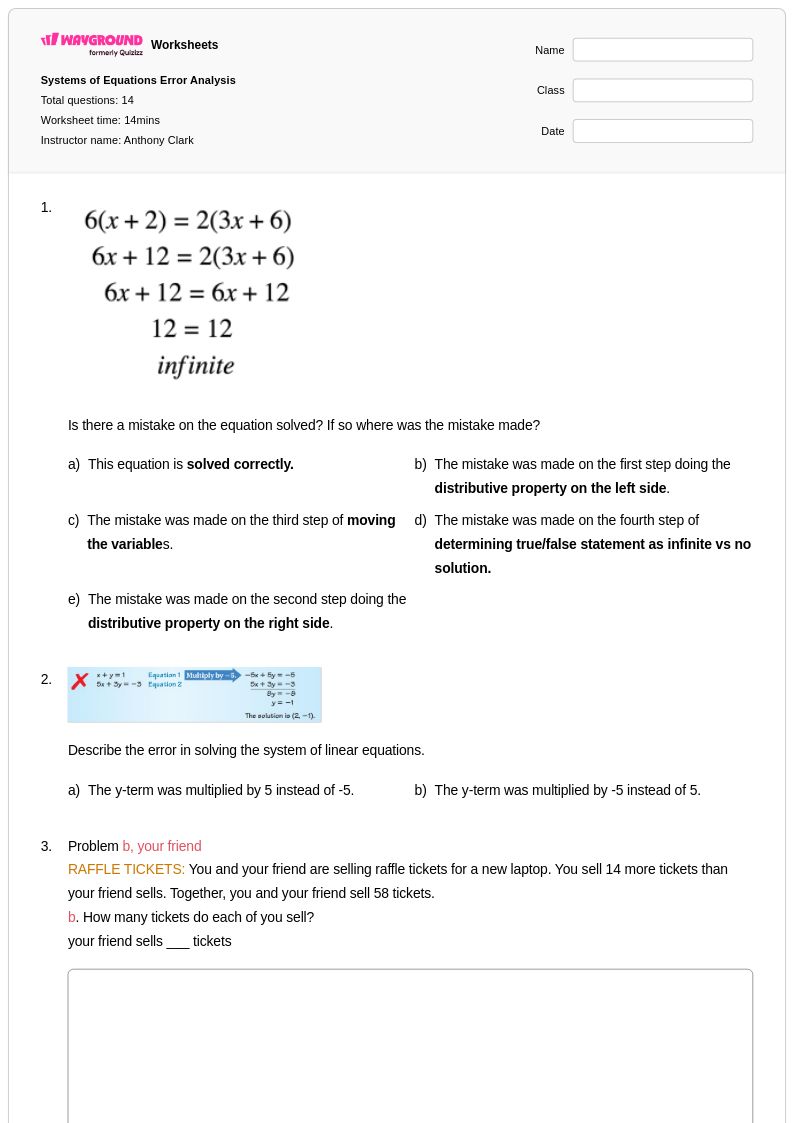
14Q
9th - Uni
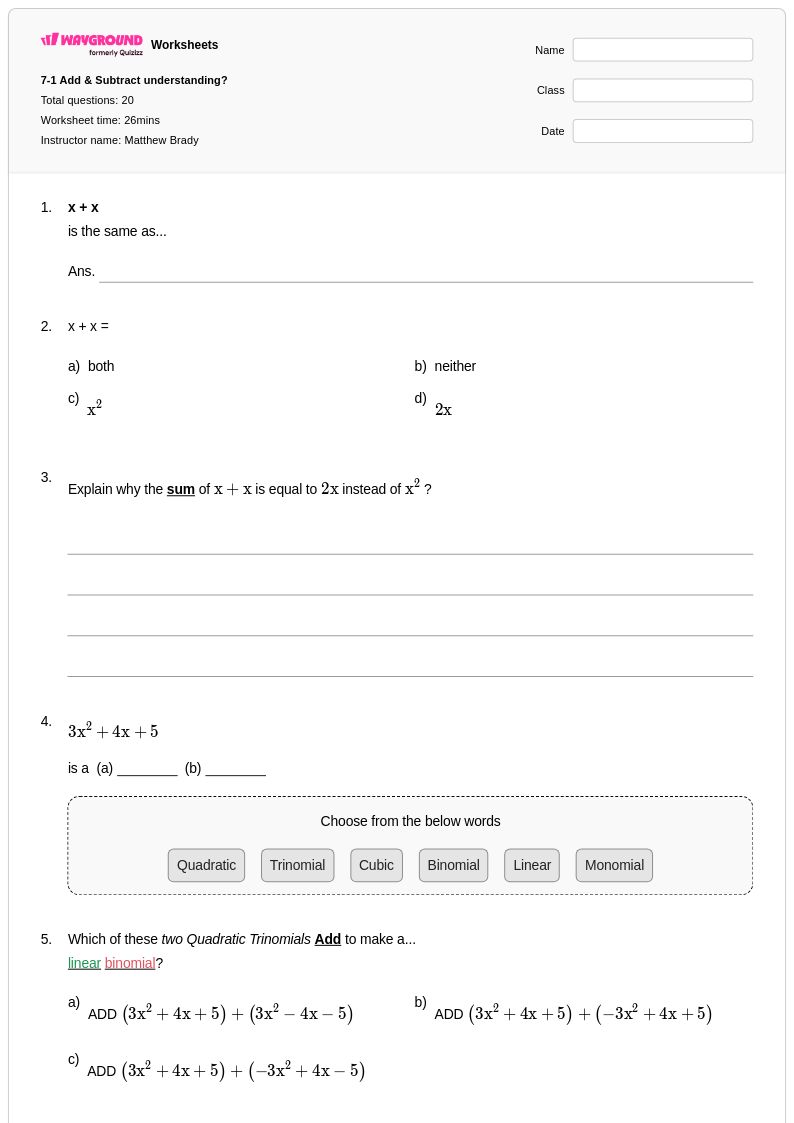
20Q
9th - 12th

11Q
9th - 12th

20Q
7th - Uni

20Q
7th - Uni
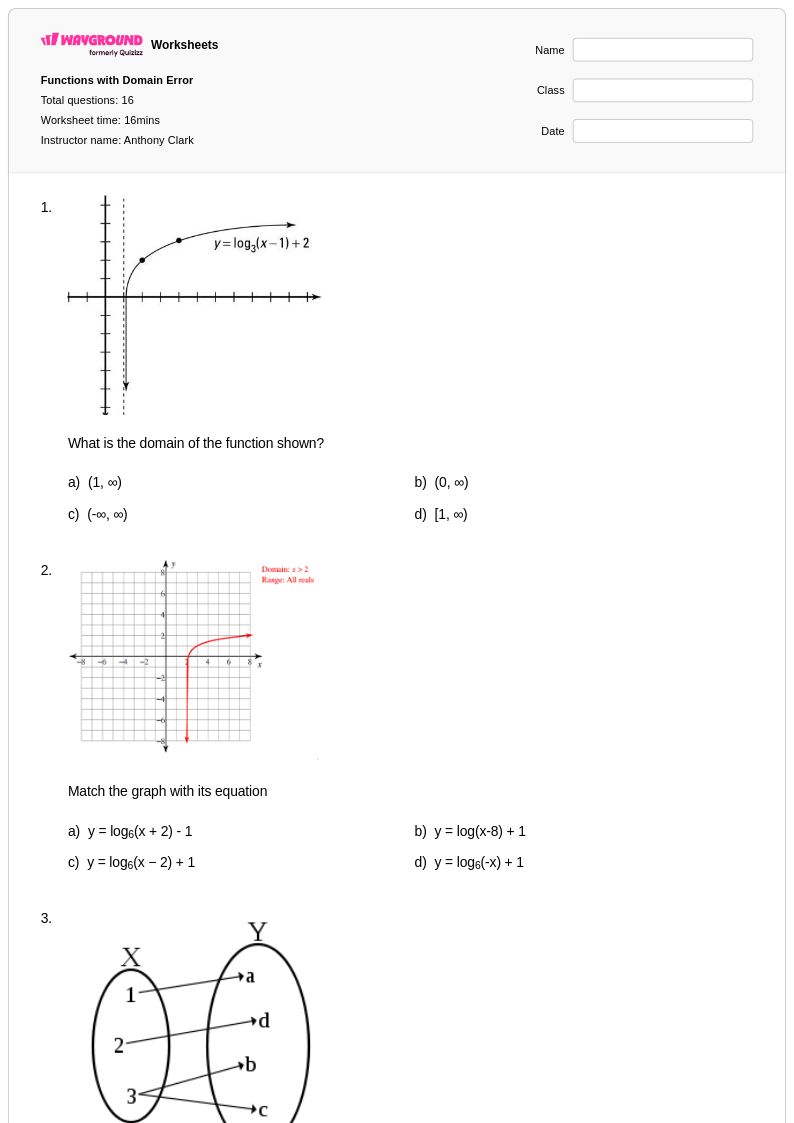
16Q
9th - Uni
20Q
9th - Uni
Explore outras planilhas de assuntos para ระดับ 10
สำรวจแผ่นงาน ขอบเขตข้อผิดพลาดของลากรางจ์ ที่พิมพ์ได้สำหรับ ชั้นประถมศึกษาปีที่ 10
แบบฝึกหัดขอบเขตความคลาดเคลื่อนของลากรางจ์สำหรับนักเรียนชั้นมัธยมศึกษาปีที่ 4 (เกรด 10) เป็นแบบฝึกหัดที่สำคัญยิ่งในแนวคิดทางทฤษฎีที่สำคัญที่สุดอย่างหนึ่งของแคลคูลัส ช่วยให้นักเรียนเข้าใจวิธีการวัดความแม่นยำของการประมาณค่าด้วยพหุนามเทย์เลอร์ แบบฝึกหัดที่ครอบคลุมเหล่านี้จะแนะนำนักเรียนผ่านกระบวนการที่เป็นระบบของการใช้สูตรเศษเหลือของลากรางจ์เพื่อกำหนดความคลาดเคลื่อนสูงสุดที่เป็นไปได้เมื่อใช้ชุดอนุกรมเทย์เลอร์ในการประมาณค่าฟังก์ชัน นักเรียนจะได้ทำแบบฝึกหัดที่มีโครงสร้างอย่างรอบคอบ ซึ่งจะช่วยเสริมสร้างความเข้าใจในการหาขอบเขตที่เหมาะสมสำหรับอนุพันธ์ การกำหนดช่วงความถูกต้อง และการคำนวณค่าประมาณความคลาดเคลื่อนที่แม่นยำ แบบฝึกหัดแต่ละชุดประกอบด้วยเฉลยคำตอบโดยละเอียดและวิธีแก้ปัญหาทีละขั้นตอน ซึ่งช่วยให้นักเรียนตรวจสอบงานของตนเองและระบุส่วนที่ต้องการการเน้นเพิ่มเติม โดยมีสื่อการเรียนรู้ให้ใช้งานในรูปแบบไฟล์พิมพ์ฟรีและไฟล์ PDF ที่ดาวน์โหลดได้ ซึ่งสนับสนุนทั้งการเรียนการสอนในห้องเรียนและการเรียนรู้ด้วยตนเอง
Wayground (เดิมชื่อ Quizizz) ช่วยเสริมศักยภาพให้กับครูผู้สอนคณิตศาสตร์ด้วยแบบฝึกหัดขอบเขตความคลาดเคลื่อนของลากรางจ์นับล้านชุดที่สร้างโดยครูผู้สอนโดยเฉพาะ ซึ่งออกแบบมาสำหรับการสอนแคลคูลัสชั้นมัธยมศึกษาปีที่ 4 (เกรด 10) แพลตฟอร์มนี้มีฟังก์ชันการค้นหาและการกรองขั้นสูง ช่วยให้ครูสามารถค้นหาแบบฝึกหัดที่สอดคล้องกับมาตรฐานหลักสูตรและวัตถุประสงค์การเรียนรู้ได้อย่างรวดเร็ว ในขณะที่เครื่องมือปรับระดับความยากง่ายในตัว ช่วยให้สามารถปรับแต่งแบบฝึกหัดสำหรับนักเรียนที่มีระดับทักษะแตกต่างกันได้อย่างราบรื่น แบบฝึกหัดเหล่านี้มีให้เลือกทั้งแบบพิมพ์และแบบดิจิทัล รวมถึงไฟล์ PDF ที่จัดรูปแบบอย่างมืออาชีพ ซึ่งรักษาความถูกต้องของสัญลักษณ์ทางคณิตศาสตร์บนอุปกรณ์และระบบการพิมพ์ต่างๆ ครูสามารถวางแผนบทเรียนได้อย่างมีประสิทธิภาพ สร้างสื่อเสริมสำหรับนักเรียนที่เรียนอ่อน พัฒนากิจกรรมเสริมสำหรับผู้เรียนที่มีความสามารถสูง และให้การฝึกฝนทักษะอย่างเป็นระบบเพื่อสร้างความมั่นใจในแนวคิดแคลคูลัสที่ท้าทายนี้ ผ่านชุดโจทย์ปัญหาที่เป็นระบบและค่อยเป็นค่อยไป
