22Q
5th
18Q
5th

20Q
5th

20Q
3rd - Uni
20Q
5th - Uni
20Q
5th - Uni
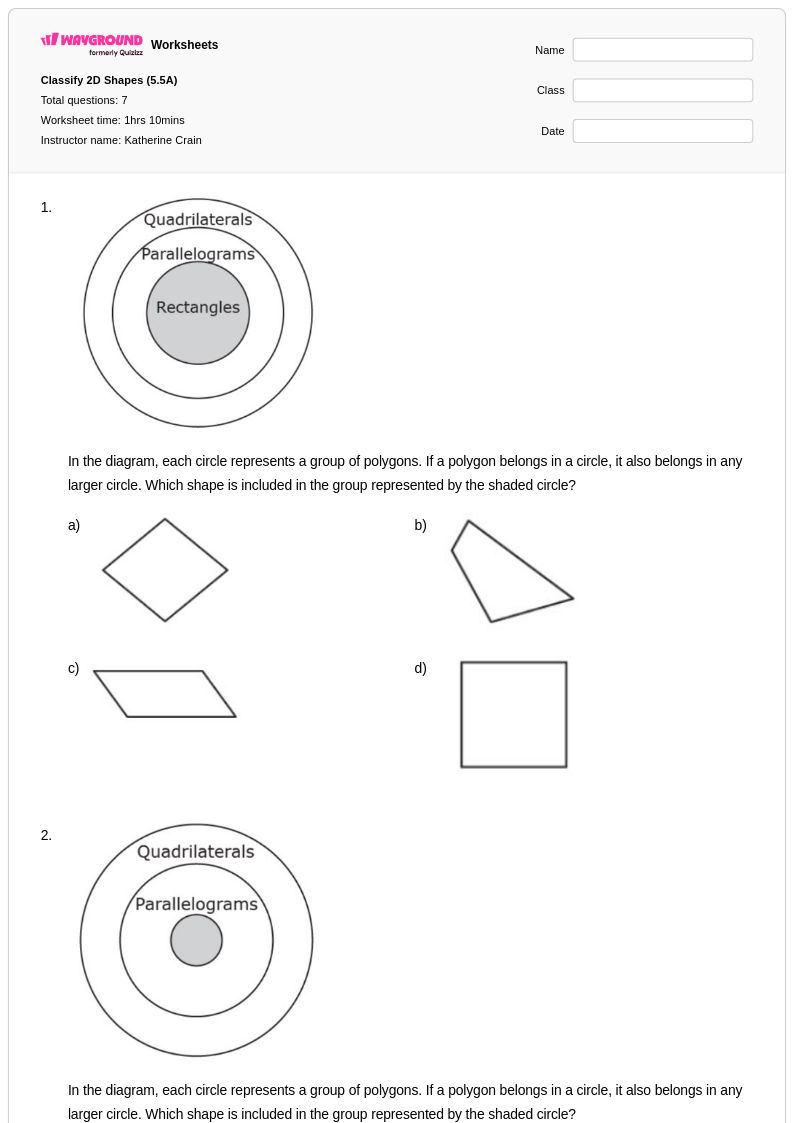
7Q
5th

20Q
5th - Uni
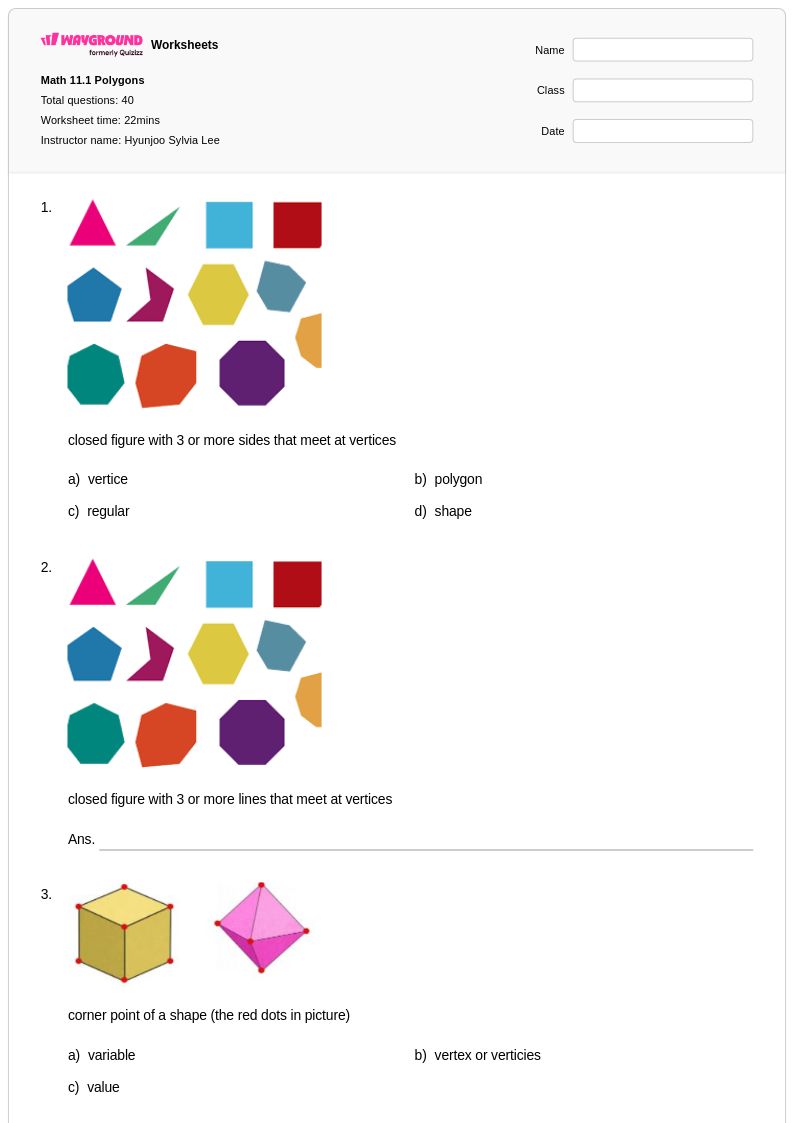
40Q
3rd - 5th
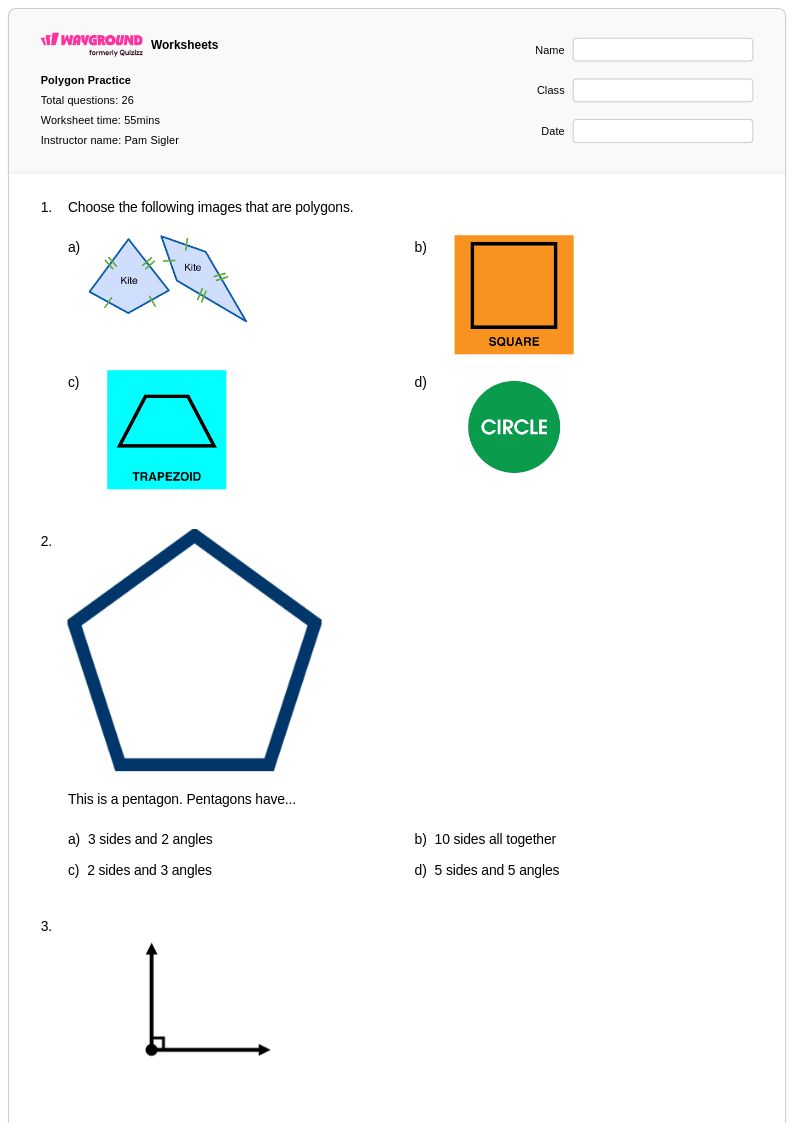
26Q
5th
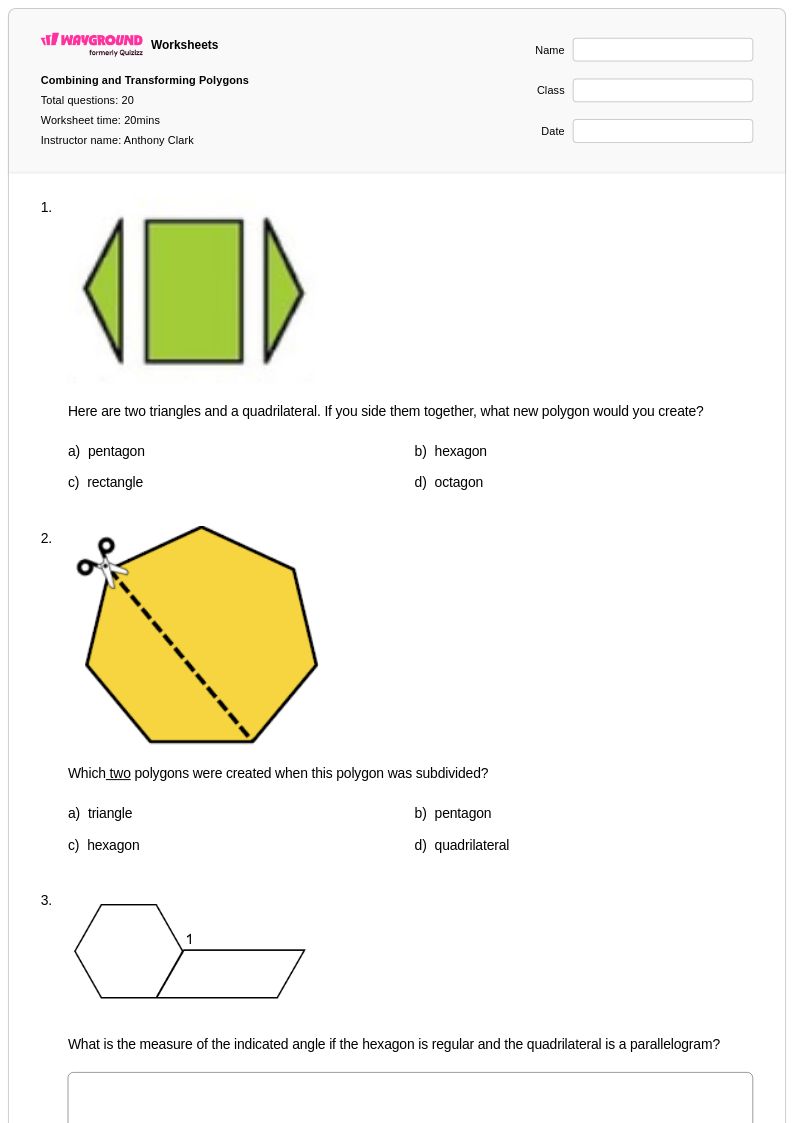
20Q
5th - Uni

14Q
3rd - Uni

20Q
3rd - Uni
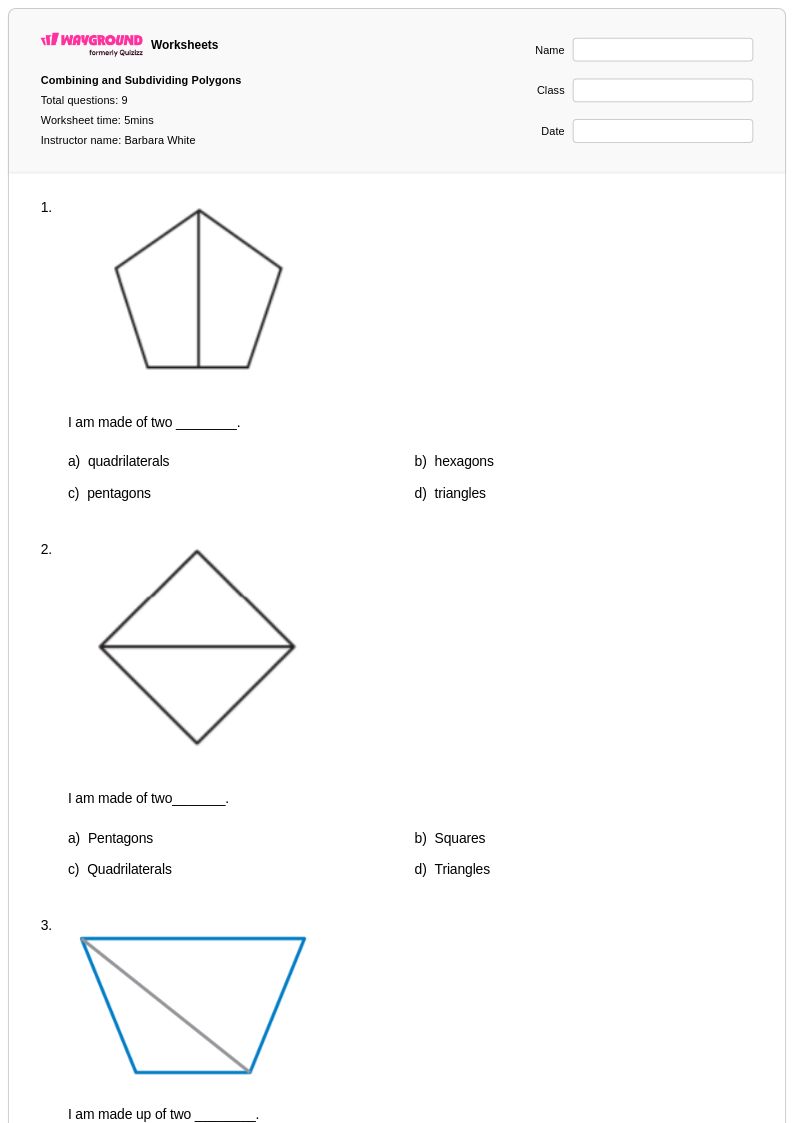
9Q
5th
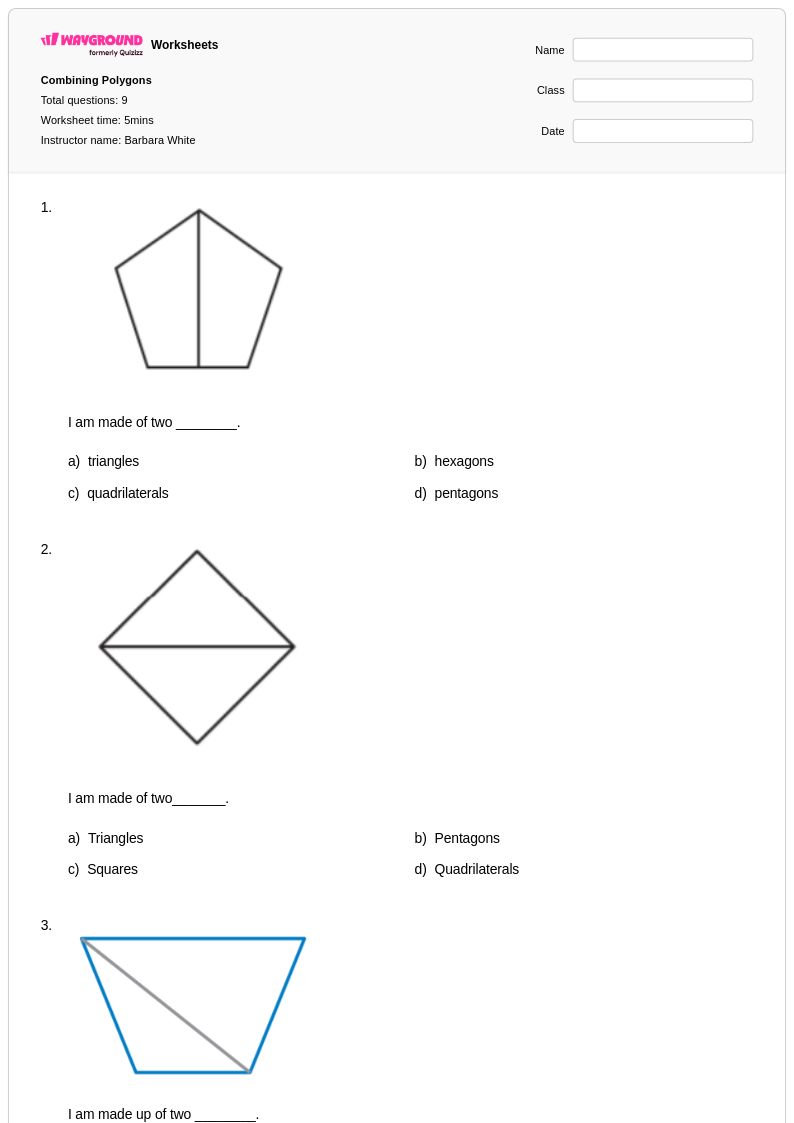
9Q
5th

19Q
5th - Uni
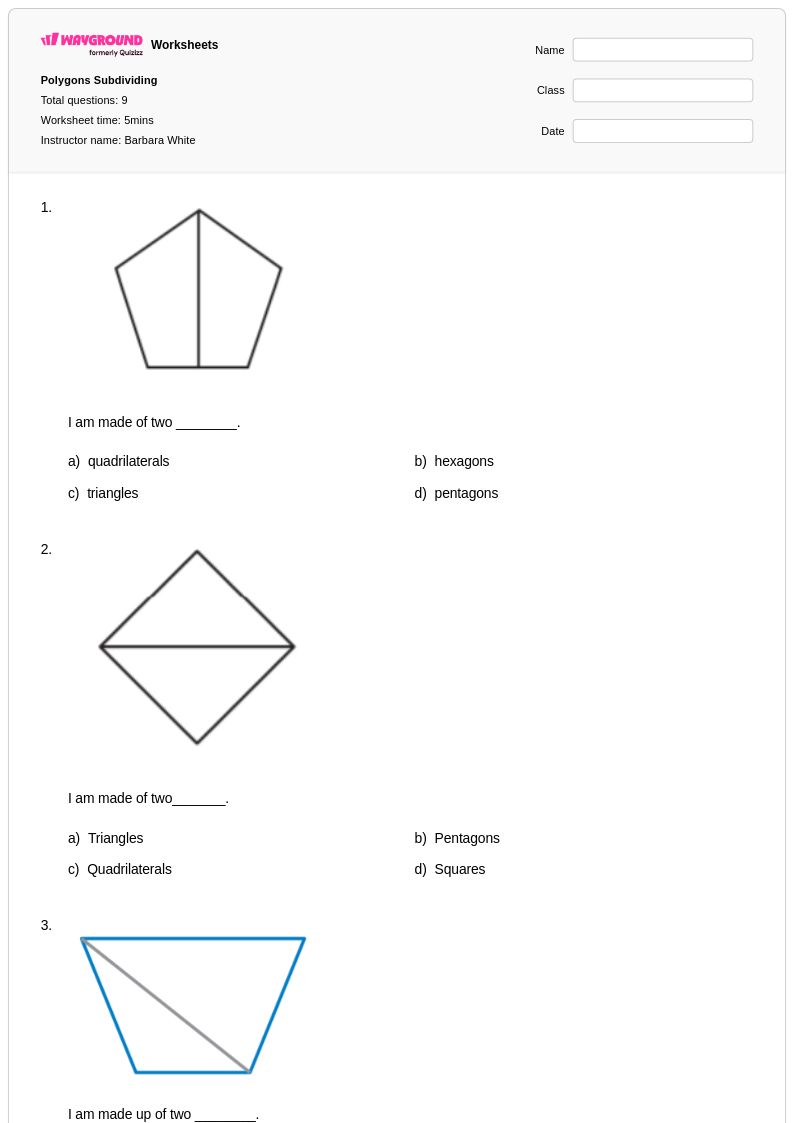
9Q
5th
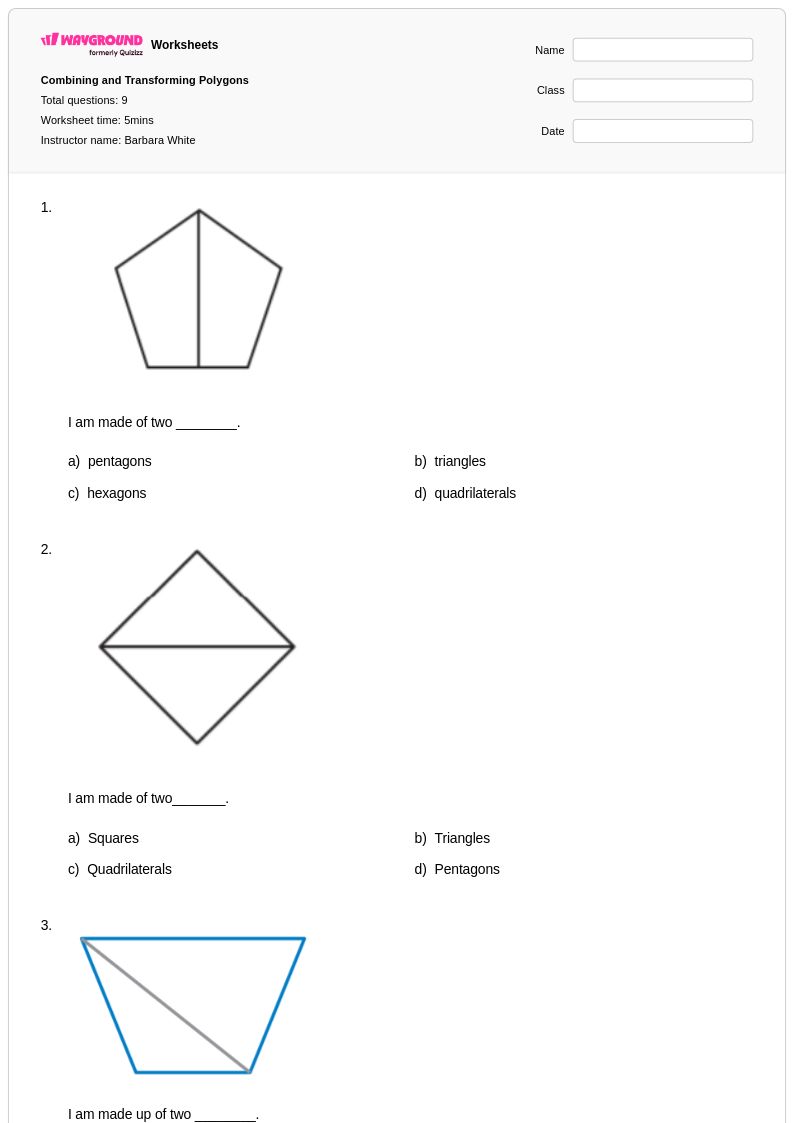
9Q
5th
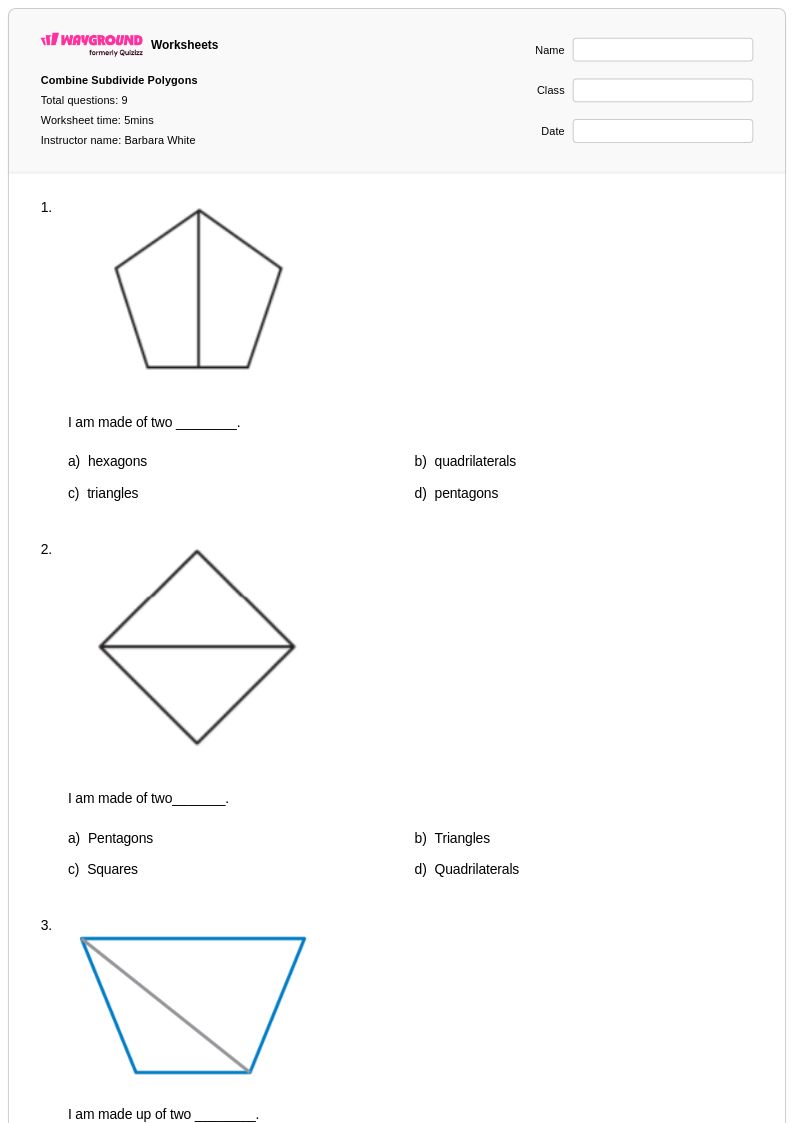
9Q
5th
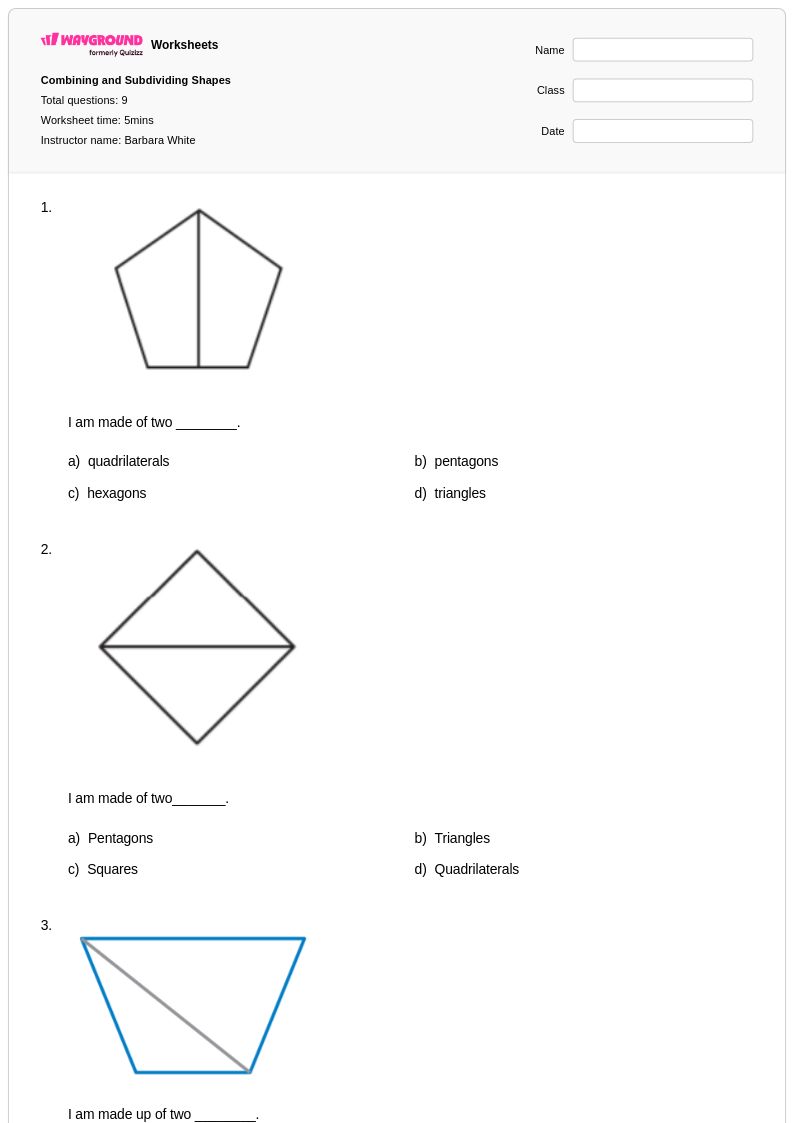
9Q
5th
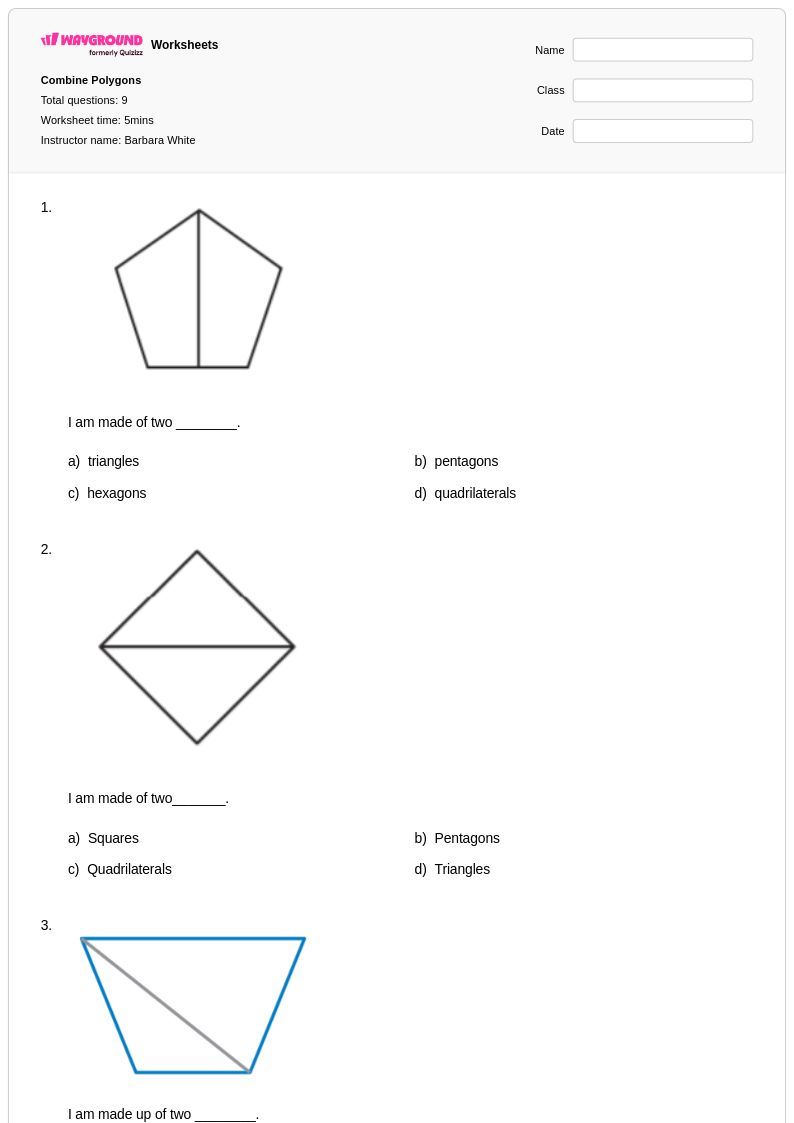
9Q
5th
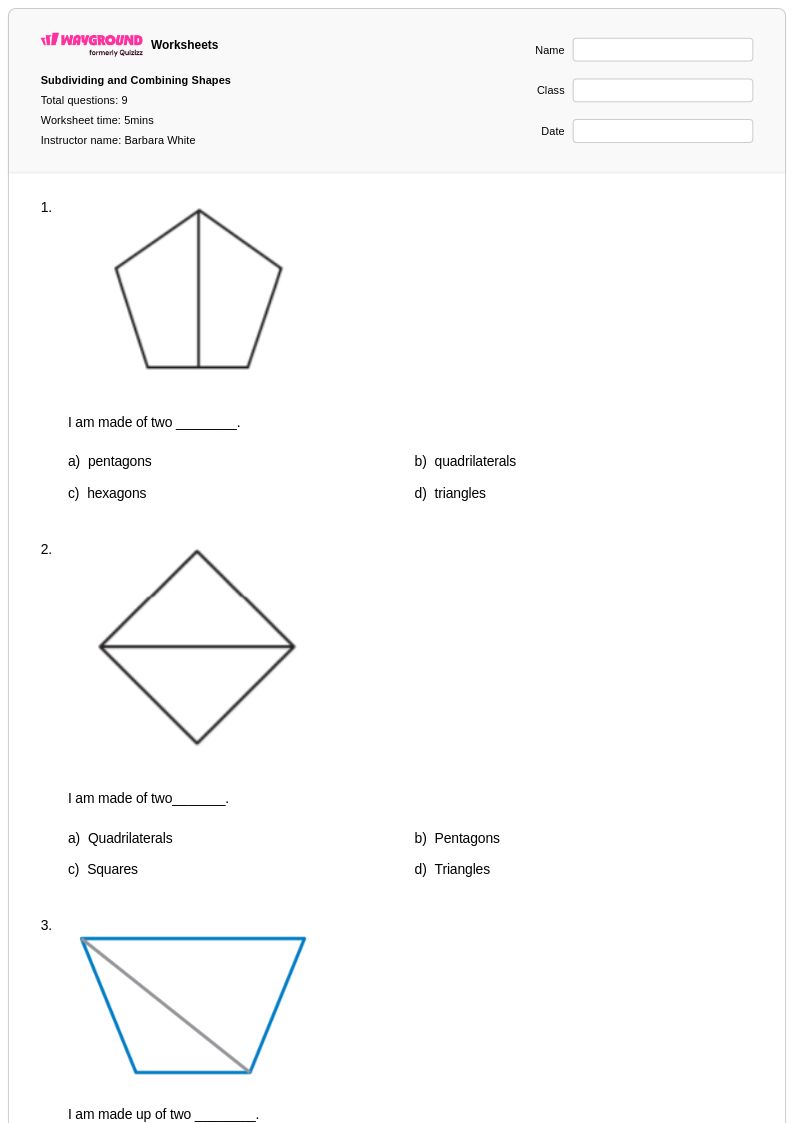
9Q
5th
7Q
5th

20Q
3rd - Uni
Explore outras planilhas de assuntos para ระดับ 5
สำรวจแผ่นงาน เพนตากอน ที่พิมพ์ได้สำหรับ ชั้นประถมศึกษาปีที่ 5
แบบฝึกหัดรูปห้าเหลี่ยมสำหรับวิชาคณิตศาสตร์ชั้นประถมศึกษาปีที่ 5 ช่วยให้นักเรียนได้ฝึกฝนอย่างครอบคลุมในการระบุ วิเคราะห์ และทำความเข้าใจคุณสมบัติของรูปห้าเหลี่ยมในบริบทที่กว้างขึ้นของเรขาคณิตสองมิติ แบบฝึกหัดที่ออกแบบมาอย่างพิถีพิถันเหล่านี้ช่วยให้นักเรียนพัฒนาทักษะการให้เหตุผลทางเรขาคณิตที่สำคัญโดยการสำรวจลักษณะของรูปห้าเหลี่ยม เช่น มุมภายใน ความยาวด้าน และคุณสมบัติสมมาตร ชุดแบบฝึกหัดที่มีให้ใช้งานผ่าน Wayground มีเฉลยคำตอบที่ช่วยให้การเรียนรู้ด้วยตนเองและการประเมินตนเองเป็นไปได้ง่ายขึ้น ในขณะที่รูปแบบ PDF ที่พิมพ์ได้ช่วยให้การแจกจ่ายในห้องเรียนและการมอบหมายการบ้านทำได้ง่าย นักเรียนจะเสริมสร้างความสามารถในการมองเห็นภาพเชิงพื้นที่และคำศัพท์ทางเรขาคณิตขณะที่พวกเขาทำแบบฝึกหัดฟรีที่หลากหลาย ตั้งแต่การระบุรูปห้าเหลี่ยมขั้นพื้นฐานไปจนถึงปัญหาที่ซับซ้อนมากขึ้นเกี่ยวกับการสร้างและการวัดรูปห้าเหลี่ยม
คลังทรัพยากรรูปห้าเหลี่ยมที่สร้างโดยครูจำนวนมากของ Wayground มาจากผลงานของครูผู้สอนนับล้านคน ทำให้ครูผู้สอนคณิตศาสตร์ชั้นประถมศึกษาปีที่ 5 มีความสามารถในการค้นหาและกรองข้อมูลอย่างมีประสิทธิภาพเพื่อค้นหาสื่อที่สอดคล้องกับมาตรฐานหลักสูตรและวัตถุประสงค์การเรียนรู้ที่เฉพาะเจาะจง เครื่องมือปรับระดับความยากง่ายของแพลตฟอร์มนี้ช่วยให้ครูสามารถปรับแต่งแบบฝึกหัดรูปห้าเหลี่ยมตามความต้องการของนักเรียนแต่ละคน โดยให้การสนับสนุนเพิ่มเติมสำหรับนักเรียนที่เรียนรู้ช้า และโอกาสในการเสริมสร้างความรู้สำหรับนักเรียนที่เรียนรู้เร็ว แหล่งข้อมูลที่ยืดหยุ่นเหล่านี้มีให้เลือกทั้งแบบพิมพ์ได้และแบบดิจิทัล รวมถึงไฟล์ PDF ที่ดาวน์โหลดได้ ซึ่งช่วยให้การบูรณาการเข้ากับการวางแผนบทเรียนและการบ้านเป็นไปอย่างราบรื่น ครูสามารถจัดการกับรูปแบบการเรียนรู้และระดับการศึกษาที่หลากหลายได้อย่างมีประสิทธิภาพ ในขณะเดียวกันก็มั่นใจได้ว่ามีการฝึกฝนทักษะอย่างสม่ำเสมอในการจดจำรูปห้าเหลี่ยม การวิเคราะห์คุณสมบัติ และเทคนิคการแก้ปัญหาทางเรขาคณิต ซึ่งจะสร้างความเข้าใจพื้นฐานสำหรับแนวคิดทางเรขาคณิตขั้นสูงต่อไป
