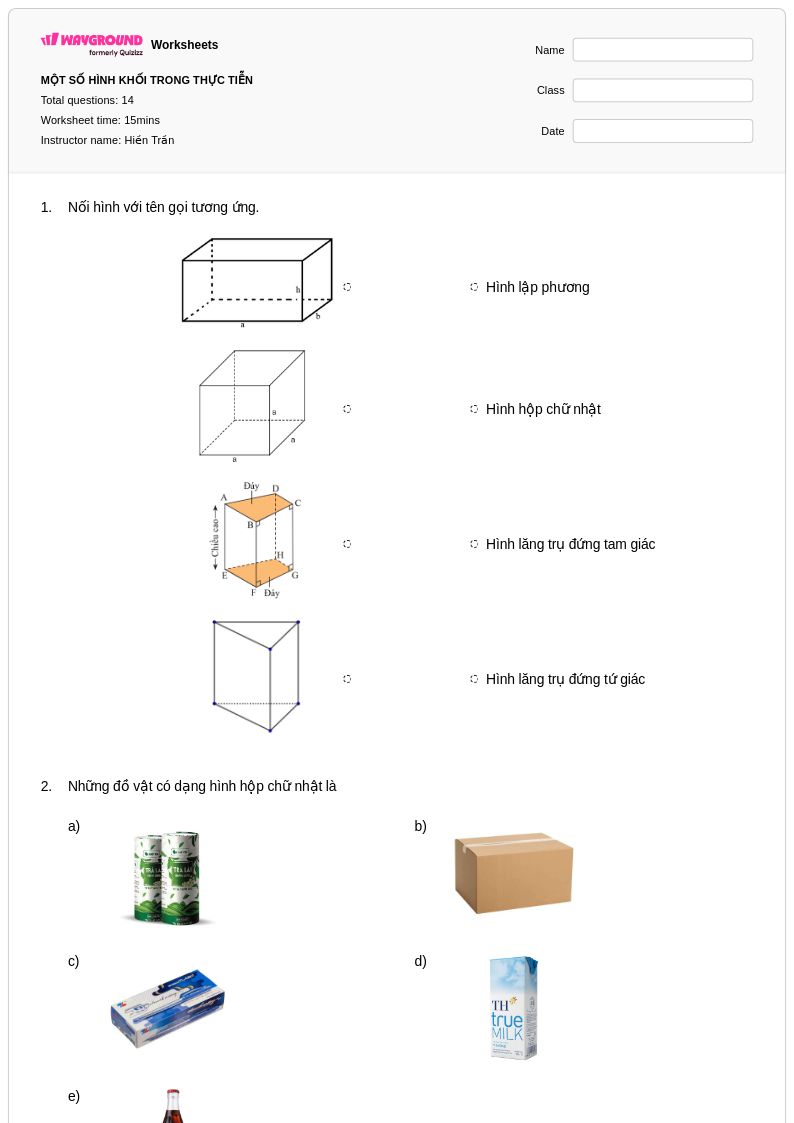
14Q
7th

10Q
1st - 12th

10Q
7th

15Q
7th - 8th

10Q
7th

10Q
7th

11Q
7th

37Q
7th

12Q
7th

20Q
7th

15Q
7th
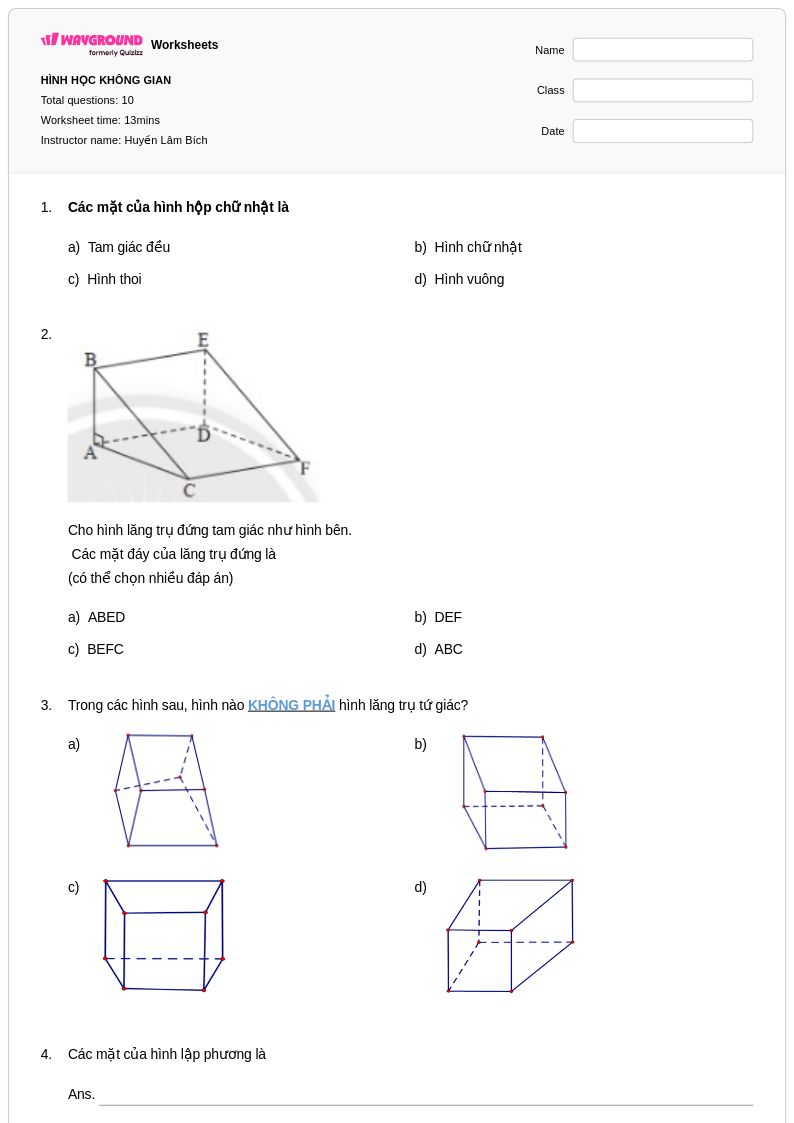
10Q
6th - 8th

8Q
7th

8Q
1st - 8th

20Q
7th

24Q
KG - PD

20Q
7th

10Q
7th

25Q
7th

22Q
7th

6Q
7th

20Q
2nd - 7th

10Q
6th - 9th

10Q
7th
Explore outras planilhas de assuntos para lớp 7
Khám phá các trang tính Công thức truy hồi có thể in được cho Lớp 7
Công thức truy hồi trong toán lớp 7 là một khái niệm nền tảng, nơi học sinh học cách định nghĩa dãy số bằng cách biểu diễn mỗi số hạng liên quan đến các số hạng trước đó. Bộ sưu tập bài tập công thức truy hồi toàn diện của Wayground cung cấp cho học sinh lớp 7 các bài toán thực hành có cấu trúc, giúp xây dựng sự hiểu biết về cách các quy luật xuất hiện khi mỗi số hạng phụ thuộc vào các giá trị trước đó. Những bài tập được thiết kế cẩn thận này củng cố các kỹ năng tư duy toán học quan trọng bằng cách yêu cầu học sinh xác định mối quan hệ giữa các số hạng liên tiếp, viết định nghĩa truy hồi và tạo ra các giá trị dãy số từng bước một. Mỗi bài tập đều bao gồm đáp án đầy đủ, giúp giáo viên dễ dàng đánh giá tiến độ học tập của học sinh và cung cấp phản hồi cụ thể về khái niệm đại số thiết yếu này, giúp kết nối dãy số học với lý luận toán học nâng cao hơn.
Wayground, trước đây là Quizizz, hỗ trợ giáo viên toán học với hàng triệu tài nguyên do giáo viên tạo ra, tập trung cụ thể vào các chủ đề về dãy số và chuỗi số như công thức truy hồi. Khả năng tìm kiếm và lọc mạnh mẽ của nền tảng cho phép giáo viên nhanh chóng tìm thấy các tài liệu phù hợp với lớp 7, phù hợp với các tiêu chuẩn chương trình giảng dạy và trình độ kỹ năng của học sinh. Những bộ sưu tập bài tập đa năng này hỗ trợ việc giảng dạy phân hóa thông qua các mức độ khó có thể tùy chỉnh và có thể được tích hợp liền mạch vào kế hoạch bài học để giới thiệu khái niệm ban đầu, củng cố kỹ năng hoặc các hoạt động nâng cao. Có sẵn ở cả định dạng kỹ thuật số và PDF có thể in, các tài nguyên này cung cấp sự linh hoạt cho việc sử dụng trong lớp học, bài tập về nhà và các buổi thực hành độc lập, đảm bảo rằng học sinh phát triển các kỹ năng nền tảng vững chắc trong việc nhận biết và áp dụng các mẫu đệ quy trong nhiều ngữ cảnh toán học khác nhau.
