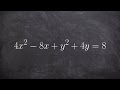
Completing the Square and Quadratics
Interactive Video
•
Mathematics, Science, Education
•
9th - 12th Grade
•
Hard
Amelia Wright
FREE Resource
Read more
10 questions
Show all answers
1.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
Why is it important to rewrite a quadratic in standard form when graphing an ellipse?
To make the equation linear
To eliminate variables
To easily identify the center and vertices
To simplify the equation
2.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the first step in organizing the variables in the given equation?
Combine all terms on one side
Separate the x and y terms
Factor out common terms
Add constants to both sides
3.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the purpose of completing the square in the context of this lesson?
To convert a binomial into a trinomial
To create a perfect square trinomial
To eliminate the constant term
To factor out the leading coefficient
4.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What does the term 'binomial squared' refer to in this context?
A trinomial rewritten as a square of a binomial
A polynomial with two terms
A quadratic equation
A linear equation
5.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
When completing the square, what value do you add to both sides of the equation?
The coefficient of x
The square of half the coefficient of x
The constant term
The product of the coefficients of x and y
6.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
Why must you adjust the equation after adding values to complete the square?
To factor out common terms
To eliminate the constant term
To simplify the equation
To maintain the balance of the equation
7.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the result of factoring out a 4 from the term 4x^2 - 8x?
x(x - 2)
x^2 - 2x
4(x^2 - 2x)
4x(x - 2)
Create a free account and access millions of resources
Similar Resources on Wayground

11 questions
Understanding Polar Equations and Ellipses
Interactive video
•
9th - 12th Grade

11 questions
Understanding Conic Sections and Their Properties
Interactive video
•
9th - 12th Grade

11 questions
Understanding Hyperbolas
Interactive video
•
9th - 12th Grade

11 questions
Understanding Ellipses
Interactive video
•
8th - 12th Grade

11 questions
Graphing and Analyzing Ellipses
Interactive video
•
9th - 10th Grade

11 questions
Understanding Parabolas and Their Properties
Interactive video
•
9th - 12th Grade

11 questions
Understanding Conic Sections and Circles
Interactive video
•
8th - 12th Grade

11 questions
Ellipse and Angle Relationships
Interactive video
•
9th - 12th Grade
Popular Resources on Wayground

10 questions
Video Games
Quiz
•
6th - 12th Grade

10 questions
Lab Safety Procedures and Guidelines
Interactive video
•
6th - 10th Grade

25 questions
Multiplication Facts
Quiz
•
5th Grade

10 questions
UPDATED FOREST Kindness 9-22
Lesson
•
9th - 12th Grade

22 questions
Adding Integers
Quiz
•
6th Grade

15 questions
Subtracting Integers
Quiz
•
7th Grade

20 questions
US Constitution Quiz
Quiz
•
11th Grade

10 questions
Exploring Digital Citizenship Essentials
Interactive video
•
6th - 10th Grade
Discover more resources for Mathematics

15 questions
ACT Math Practice Test
Quiz
•
9th - 12th Grade

12 questions
Graphing Inequalities on a Number Line
Quiz
•
9th Grade

15 questions
Two Step Equations
Quiz
•
9th Grade

15 questions
Combining Like Terms and Distributive Property
Quiz
•
9th Grade

12 questions
Absolute Value Equations
Quiz
•
9th Grade

8 questions
ACT Math Strategies
Lesson
•
9th Grade

10 questions
Solving Absolute Value Equations
Quiz
•
9th Grade

16 questions
Parallel Lines Cut by a Transversal
Lesson
•
9th - 10th Grade