What are the two possible orientations of a parabola in conic sections?
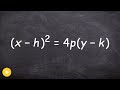
Understanding Parabolas in Conic Sections
Interactive Video
•
Sophia Harris
•
Mathematics, Science
•
8th - 12th Grade
•
11 plays
•
Medium
Read more
10 questions
Show all answers
1.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
Circular and elliptical
Horizontal and diagonal
Vertical and diagonal
Vertical and horizontal
2.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
In the vertex form of a parabola, what do the variables h and k represent?
The axis of symmetry
The vertex of the parabola
The focal length and width
The focus and directrix
3.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
How is the orientation of a parabola determined in its equation?
By the presence of a directrix
By the constant term
By the variable that is squared
By the coefficient of the linear term
4.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the focus of a parabola?
A line perpendicular to the directrix
A point equidistant from the vertex and directrix
A line parallel to the axis of symmetry
A point inside the parabola
5.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What role does the value 'p' play in determining the focus and directrix?
It represents the slope of the parabola
It is the distance from the vertex to the focus
It determines the width of the parabola
It is the midpoint of the parabola
6.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
For a vertical parabola, how is the directrix expressed?
As a diagonal line
As a horizontal line
As a vertical line
As a point
7.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
How do you find the focus of a vertical parabola?
By subtracting p from the y-coordinate of the vertex
By adding p to the y-coordinate of the vertex
By adding p to the x-coordinate of the vertex
By subtracting p from the x-coordinate of the vertex
8.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
In a horizontal parabola, how is the directrix expressed?
As a point
As a diagonal line
As a vertical line
As a horizontal line
9.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the focal length in the context of parabolas?
The distance from the vertex to the directrix
The width of the parabola
The distance from the focus to the directrix
The distance from the vertex to the focus
10.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the focal width of a parabola?
The width of the parabola at its base
The distance from the vertex to the focus
The distance from the vertex to the directrix
The distance across the parabola through the focus
Explore all questions with a free account
Similar Resources on Quizizz

11 questions
Conic Sections and Their Properties
Interactive video
•
9th - 12th Grade

11 questions
Parabola Properties and Equations
Interactive video
•
7th - 10th Grade

8 questions
What you need to know parabola in conic section
Interactive video
•
9th - 10th Grade

11 questions
Understanding Parabolas: Focus and Directrix
Interactive video
•
9th - 12th Grade

11 questions
Understanding Parabolas: Vertex, Focus, and Directrix
Interactive video
•
9th - 12th Grade

11 questions
Understanding Parabolas and Their Properties
Interactive video
•
9th - 12th Grade

11 questions
Understanding Parabolas: Vertex, Focus, and Directrix
Interactive video
•
9th - 12th Grade

11 questions
Parabola Properties and Equations
Interactive video
•
9th - 12th Grade
Popular Resources on Quizizz

17 questions
CAASPP Math Practice 3rd
Quiz
•
3rd Grade

20 questions
math review
Quiz
•
4th Grade

21 questions
6th Grade Math CAASPP Practice
Quiz
•
6th Grade

13 questions
Cinco de mayo
Interactive video
•
6th - 8th Grade

20 questions
Reading Comprehension
Quiz
•
5th Grade

20 questions
Types of Credit
Quiz
•
9th - 12th Grade

10 questions
4th Grade Math CAASPP (part 1)
Quiz
•
4th Grade

45 questions
5th Grade CAASPP Math Review
Quiz
•
5th Grade
Discover more resources for Mathematics

12 questions
2024 Keystone Algebra I Module I Sampler
Quiz
•
9th Grade

37 questions
Math 8 SOL Review
Quiz
•
8th Grade

5 questions
8.MG.1-5 Quizizz Day 3
Quiz
•
6th - 8th Grade

21 questions
8th Grade math review
Quiz
•
8th Grade

21 questions
Scatter Plots
Quiz
•
8th Grade

31 questions
Grade 8 FAST MATH Review
Quiz
•
8th Grade

5 questions
8.NNS/CE Quizizz Day 2
Quiz
•
6th - 8th Grade

20 questions
Parallel Lines Cut by a Transversal
Quiz
•
8th Grade