What is the first step in solving an exponential equation using logarithms?
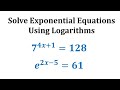
Solving Exponential and Logarithmic Equations
Interactive Video
•
Aiden Montgomery
•
Mathematics
•
9th - 12th Grade
•
Hard
Read more
10 questions
Show all answers
1.
MULTIPLE CHOICE
30 sec • 1 pt
2.
MULTIPLE CHOICE
30 sec • 1 pt
In the equation 7^(4x + 1) = 128, what logarithm is used to solve for x?
3.
MULTIPLE CHOICE
30 sec • 1 pt
What property of logarithms allows us to move the exponent to the front?
4.
MULTIPLE CHOICE
30 sec • 1 pt
After applying the power property, what is the next step in solving for x in the equation 7^(4x + 1) = 128?
5.
MULTIPLE CHOICE
30 sec • 1 pt
What is the approximate value of x in the equation 7^(4x + 1) = 128?
6.
MULTIPLE CHOICE
30 sec • 1 pt
In the equation e^(2x - 5) = 61, why is the natural logarithm preferred?
7.
MULTIPLE CHOICE
30 sec • 1 pt
What is the value of natural log e?
8.
MULTIPLE CHOICE
30 sec • 1 pt
What is the next step after simplifying 2x - 5 = natural log 61?
9.
MULTIPLE CHOICE
30 sec • 1 pt
What is the approximate value of x in the equation e^(2x - 5) = 61?
10.
MULTIPLE CHOICE
30 sec • 1 pt
How can you verify the solution for x in the equation e^(2x - 5) = 61?
Explore all questions with a free account
Similar Resources on Quizizz

11 questions
Logarithmic and Exponential Concepts
•
9th - 12th Grade

11 questions
Natural Logarithms and Exponential Functions
•
9th - 12th Grade

9 questions
Logarithmic Equations and Exponents
•
9th - 12th Grade

11 questions
Understanding Exponential Expressions and Logarithms
•
9th - 12th Grade

11 questions
Solving Exponential and Logarithmic Equations
•
9th - 12th Grade

11 questions
Exploring Logarithm Solutions: Part 1
•
8th - 12th Grade

11 questions
Solving Exponential and Logarithmic Equations
•
9th - 12th Grade

9 questions
Understanding Logarithms and Exponentials
•
9th - 12th Grade
Popular Resources on Quizizz

17 questions
CAASPP Math Practice 3rd
•
3rd Grade

15 questions
Grade 3 Simulation Assessment 1
•
3rd Grade

20 questions
math review
•
4th Grade

19 questions
HCS Grade 5 Simulation Assessment_1 2425sy
•
5th Grade

16 questions
Grade 3 Simulation Assessment 2
•
3rd Grade

21 questions
6th Grade Math CAASPP Practice
•
6th Grade

13 questions
Cinco de mayo
•
6th - 8th Grade

20 questions
Reading Comprehension
•
5th Grade
Discover more resources for Mathematics

15 questions
Algebra 1 EOC Review #1
•
9th Grade

15 questions
Independent and Dependent Probability
•
9th Grade

14 questions
Algebra 1 SOL Review #1
•
9th Grade

20 questions
Algebra 1 EOC Review 1
•
9th Grade

15 questions
Algebra 1 SOL Review #2
•
9th Grade

5 questions
A.EI.1-3 Quizizz Day 4
•
9th - 12th Grade

5 questions
A.EI.1-3 Quizizz Day 2
•
9th - 12th Grade

20 questions
Quadratic Formula
•
9th Grade