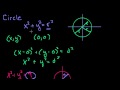
Understanding Conic Sections: Circles

The video tutorial explains conic sections, focusing on the circle. It covers the general equation of a circle, x^2 + y^2 = r^2, where r is the radius, and the circle is centered at (0,0). The tutorial also discusses how the equation relates to the distance formula and the Pythagorean Theorem. It then explores how to shift a circle by altering the equation to (x-h)^2 + (y-k)^2 = r^2, where (h,k) is the new center. The video emphasizes understanding these concepts to recognize and plot circles from equations.

What is the primary focus of the video on conic sections?

• Exploring the applications of conic sections in real life

• Learning to recognize and plot equations of conic sections

• Discussing the differences between various conic sections

• Understanding the history of conic sections

Tags

CCSS.HSG.GPE.A.1

What is the general equation of a circle centered at the origin?

• x^2 + y^2 = r

• x^2 + y^2 = r^2

• x^2 + y^2 = 2r

• x^2 - y^2 = r^2

Tags

CCSS.HSG.GPE.A.1

How is the radius of a circle related to its equation x^2 + y^2 = r^2?

• The radius is equal to r

• The radius is equal to 2r

• The radius is equal to r^2

• The radius is equal to the square root of r

Why can't the radius of a circle be negative?

• Because it would make the circle larger

• Because it would just mean going in the opposite direction

• Because a negative radius is not possible in geometry

• Because it would make the circle disappear

Tags

CCSS.HSG.GPE.A.1

What is the relationship between the distance formula and the circle's equation?

• The circle's equation is a complex version of the distance formula

• The circle's equation is unrelated to the distance formula

• The circle's equation is a simplification of the distance formula

• The circle's equation is derived from the distance formula

Tags

CCSS.HSG.GPE.A.1

What happens to the equation of a circle when it is shifted from the origin?

• The equation changes to include terms for the shift

• The equation remains the same

• The equation becomes linear

• The equation becomes quadratic

Tags

CCSS.8.G.A.3

CCSS.HSG.CO.A.5

If a circle is shifted to the right by 1 and down by 2, what is the new center?

• (1, -2)

• (-1, 2)

• (1, 2)

• (-1, -2)

Tags

CCSS.HSG.GPE.A.1

What is the effect of substituting x-1 and y+2 in the circle's equation?

• The circle is shifted left and up

• The circle is shifted right and down

• The circle is shifted right and up

• The circle is shifted left and down

Tags

CCSS.HSG.GPE.A.1

What is the significance of the term (x-1)^2 in the shifted circle's equation?

• It indicates a shift of the circle to the left

• It indicates a shift of the circle to the right

• It indicates a shift of the circle upwards

• It indicates a shift of the circle downwards

Tags

CCSS.HSG.CO.A.2

How can you determine the new center of a shifted circle?

• By finding the values that make the terms in the equation zero

• By adding the shift values to the original center

• By multiplying the shift values with the original center

• By subtracting the shift values from the original center

Tags

CCSS.HSG.CO.A.2