Systems of Linear Equations

What is the solution to this system?
x - y = 6
y = 2x - 5

• (1,3)

• (-1,3)

• (-1,-7)

• (1,-7)

Tags

CCSS.8.EE.C.8B

CCSS.HSA.REI.C.6

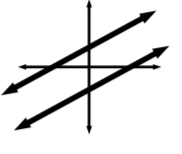
Solve the following system by graphing.  What is the solution?

• Infinite number of solutions

• (3, 3)

• (3, -3)

• (-3, 3)

Tags

CCSS.8.EE.C.8B

Solve the system by substitution. 
-2x - 2y = 16
y = -8

• (0, -8)

• (-8, 0)

• (-16, -8)

• (-16, -8)

Tags

CCSS.8.EE.C.8B

CCSS.HSA.REI.C.6

The school that Stefan goes to is selling tickets to a choral performance. On the first day of ticket sales the school sold 3 senior citizen tickets and 1 child ticket for a total of $38. The school took in $52 on the second day by selling 3 senior citizen tickets and 2 child tickets. Which equations represents the system that could be used?

• 1s + 3c = 38
  2s + 3c = 52

• 3s + 1c = 38
  3s + 2c = 52

• s + c = 38
  s + c = 52

• 3s + 3c = 38
  1s + 2c = 52

Tags

CCSS.HSA.CED.A.3

A customer at a store paid $64 for 3 large candles and 4 small candles. At the same store, a second customer paid $68 for 1 large candle and 8 small candles. The price of each large candle is the same, and the price of each small candle is the same. Which system of equations can be used to find the price in dollars of each large candle, x, and each small candle, y?

• 4y = 3x + 64

  8y = x + 68

• 4y = 3x + 64

  8y = x + 60

• 3x + 4y = 64

  x + 8y = 68

• 3x + 4y = 64

  x + 8y = 60

Tags

CCSS.HSA.CED.A.3

A customer at a store paid $64 for 3 large candles and 4 small candles. At the same store, a second customer paid $4 more than the first customer for 1 large candle and 8 small candles. The price of each large candle is the same, and the price of each small candle is the same. Which system of equations can be used to find the price in dollars of each large candle, x, and each small candle, y?

• 4y = 3x + 64

  8y = x + 68

• 4y = 3x + 64

  8y = x + 60

• 3x + 4y = 64

  x + 8y = 68

• 3x + 4y = 64

  x + 8y = 60

Tags

CCSS.8.EE.C.8C

A customer at a store paid $64 for 3 large candles and 4 small candles. At the same store, a second customer paid $4 more than the first customer for 1 large candle and 8 small candles. The price of each large candle is the same, and the price of each small candle is the same. Which system of equations can be used to find the price in dollars of each large candle, x, and each small candle, y?

• 4y = 3x + 64

  8y = x + 68

• 4y = 3x + 64

  8y = x + 60

• 3x + 4y = 64

  x + 8y = 68

• 3x + 4y = 64

  x + 8y = 60

Tags

CCSS.HSA.CED.A.3

If a system of linear equations has one solution, what does this mean about the two lines?

• Parallel lines

• the same line

• Intersecting lines

Tags

CCSS.8.EE.C.8A

Which graph represents a system of equations with infinite solutions?

• 
• 
• 
• None of the above

Tags

CCSS.8.EE.C.8B

One brand of suntan lotion comes in a small size with x ounces of lotion and a regular size with y ounces of lotion. Two small bottles plus one regular bottle contain 15 ounces of lotion, while one small bottle and two regular bottles contain 19.5 ounces of lotion. How much lotion is contained in the small bottle?

• 5 ounces

• 3.5 ounces

• 8 ounces

• 6.5

Tags

CCSS.8.EE.C.8C