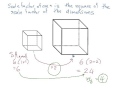
Exploring Similar and Congruent Figures

The video tutorial covers the concepts of similar and congruent figures, focusing on the role of scale factors in determining similarity. It explains how to calculate scale factors for dimensions, surface area, and volume, using pyramids and cubes as examples. The tutorial also highlights the relationship between scale factors and the geometric properties of figures, emphasizing that the scale factor for area is the square of the dimension scale factor, while for volume, it is the cube. Finally, the video briefly touches on congruent figures, which are identical in size and shape.

What is required for two pyramids to be considered similar?

• They must have the same volume.

• They must have the same surface area.

• There must be a scale factor that maps one pyramid's measurements to the other.

• They must have the same height.

If the scale factor between two similar pyramids is 3, what would be the width of the larger pyramid if the smaller one is 5 units wide?

• 15 units

• 10 units

• 8 units

• 20 units

Tags

CCSS.7.G.A.1

What is the surface area of a small cube with side length 1 unit?

• 1 square unit

• 3 square units

• 6 square units

• 12 square units

Tags

CCSS.6.G.A.4

If the scale factor for the dimensions of two cubes is 2, what is the scale factor for their surface areas?

• 8

• 2

• 4

• 6

Tags

CCSS.6.G.A.4

What is the relationship between the scale factor of dimensions and the scale factor of surface area?

• The scale factor of surface area is the same as the scale factor of dimensions.

• The scale factor of surface area is half the scale factor of dimensions.

• The scale factor of surface area is the cube of the scale factor of dimensions.

• The scale factor of surface area is the square of the scale factor of dimensions.

Tags

CCSS.7.G.B.6

What is the volume of a larger cube if the smaller cube has a volume of 1 cubic unit and the scale factor is 2?

• 8 cubic units

• 4 cubic units

• 2 cubic units

• 6 cubic units

What is the relationship between the scale factor of dimensions and the scale factor of volume?

• The scale factor of volume is the cube of the scale factor of dimensions.

• The scale factor of volume is the square of the scale factor of dimensions.

• The scale factor of volume is half the scale factor of dimensions.

• The scale factor of volume is the same as the scale factor of dimensions.

If the side length of one cube is 1.5 units and the side length of another cube is 4.5 units, what is the scale factor for their dimensions?

• 5

• 4

• 3

• 2

Tags

CCSS.7.G.A.1

If the scale factor for the dimensions of two cubes is 3, what is the scale factor for their volumes?

• 9

• 18

• 6

• 27

What does it mean for two figures to be congruent?

• They have different shapes but the same dimensions.

• They have the same volume but different shapes.

• They have the same shape and size.

• They have the same surface area but different volumes.

Tags

CCSS.8.G.A.2