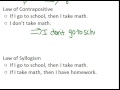
Exploring Deductive Reasoning in Geometry
Interactive Video
•
Mathematics
•
6th - 10th Grade
•
Practice Problem
•
Hard
Olivia Brooks
FREE Resource
Read more
10 questions
Show all answers
1.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is deductive reasoning based on?
Facts
Assumptions
Examples and patterns
Hypotheses
2.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
Which type of reasoning is based on examples and patterns?
Logical reasoning
Deductive reasoning
Mathematical reasoning
Inductive reasoning
3.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the conclusion if 'If I go to school, then I take math' and 'I go to school' are true?
I must not take math
I must take math
I might take math
I will not go to school
4.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What does the Law of Detachment state?
If P then Q is true, and P is true, then Q must be true
If P then Q is true, and Q is true, then P must be true
If P then Q is true, and P is false, then Q must be false
If P then Q is true, and Q is false, then P must be false
5.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the conclusion if 'If I go to school, then I take math' and 'I don't take math' are true?
I might go to school
I must not go to school
I must go to school
I will take math
6.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What does the Law of Contrapositive involve?
Combining two statements
Negating the hypothesis and conclusion
Switching the hypothesis and conclusion
Switching and negating the hypothesis and conclusion
7.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the conclusion if 'If I go to school, then I take math' and 'If I take math, then I have homework' are true?
If I go to school, then I don't have homework
If I go to school, then I have homework
If I don't take math, then I don't have homework
If I don't go to school, then I have homework
Create a free account and access millions of resources
Create resources
Host any resource
Get auto-graded reports

Continue with Google

Continue with Email

Continue with Classlink

Continue with Clever
or continue with

Microsoft
%20(1).png)
Apple
Others
Already have an account?
Similar Resources on Wayground
Popular Resources on Wayground

5 questions
This is not a...winter edition (Drawing game)
Quiz
•
1st - 5th Grade

15 questions
4:3 Model Multiplication of Decimals by Whole Numbers
Quiz
•
5th Grade

25 questions
Multiplication Facts
Quiz
•
5th Grade

10 questions
The Best Christmas Pageant Ever Chapters 1 & 2
Quiz
•
4th Grade

12 questions
Unit 4 Review Day
Quiz
•
3rd Grade

10 questions
Identify Iconic Christmas Movie Scenes
Interactive video
•
6th - 10th Grade

20 questions
Christmas Trivia
Quiz
•
6th - 8th Grade

18 questions
Kids Christmas Trivia
Quiz
•
KG - 5th Grade
Discover more resources for Mathematics

10 questions
Identify Iconic Christmas Movie Scenes
Interactive video
•
6th - 10th Grade

15 questions
Solving Equations with Variables on Both Sides Review
Quiz
•
8th Grade

15 questions
scatter plots and trend lines
Quiz
•
8th Grade

21 questions
Convert Fractions, Decimals, and Percents
Quiz
•
6th Grade

20 questions
Solving Systems of Equations by Graphing
Quiz
•
8th Grade

20 questions
Exponents
Quiz
•
6th Grade

20 questions
One step Equations
Quiz
•
6th Grade

15 questions
Christmas Movie Trivia
Quiz
•
7th Grade