Exploring the Triangle Inequality Theorem

The video tutorial explores whether any three segment lengths can form a triangle. It introduces the triangle inequality theorem, which states that the sum of any two sides of a triangle must be greater than the third side. Using GeoGebra, the video demonstrates how different segment combinations either satisfy or violate this theorem. Examples are provided to illustrate the concept, showing that not all combinations of segment lengths can form a triangle.

What is the first step in determining if three segment lengths can form a triangle?

• Measure the angles between the segments.

• Try to form a triangle with the segments.

• Arrange the segments in a line.

• Check if the segments are straight.

Tags

CCSS.7.G.A.2

What might indicate that three segment lengths cannot form a triangle?

• The segments are not straight.

• The segments are of different colors.

• Some combinations of lengths do not connect.

• The segments are too short.

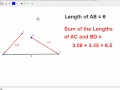
In GeoGebra, what is the fixed length of the black side of the triangle?

• 4

• 5

• 6

• 7

Tags

CCSS.HSG.MG.A.1

What happens when the sum of two sides is less than the third side in GeoGebra?

• The sides overlap.

• A triangle is formed.

• The sides cannot connect.

• The angles become acute.

According to the Triangle Inequality Theorem, what must be true for any two sides of a triangle?

• Their sum must be less than the third side.

• Their sum must be equal to the third side.

• Their sum must be twice the third side.

• Their sum must be greater than the third side.

Can a triangle be formed with side lengths 1, 2, and 4?

• No, because 1 + 2 is equal to 4.

• No, because 1 + 2 is not greater than 4.

• Yes, if the angles are adjusted.

• Yes, always.

Tags

CCSS.7.G.A.2

Why can't a triangle be formed with side lengths 1, 2, and 4?

• The sides are not straight.

• The angles are not correct.

• The sides are too short.

• The sum of 1 and 2 is not greater than 4.

Tags

CCSS.7.G.A.2

Can a triangle be formed with side lengths 2, 2, and 3?

• No, because 2 + 2 is less than 3.

• Yes, because 2 + 2 is equal to 3.

• No, because 2 + 2 is not greater than 3.

• Yes, because 2 + 2 is greater than 3.

Tags

CCSS.7.G.A.2

What is the sum of the two smallest sides in the example with side lengths 2, 2, and 3?

• 2

• 5

• 4

• 3

Tags

CCSS.7.G.A.2

What theorem is used to determine if three side lengths can form a triangle?

• Angle Sum Theorem

• Triangle Inequality Theorem

• Congruence Theorem

• Pythagorean Theorem