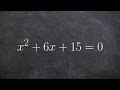
Solving Quadratic Equations with Complex Solutions

The video tutorial explains how to solve a quadratic equation that cannot be factored using the quadratic formula. It begins with setting up the problem and identifying the coefficients. The instructor discusses why factoring is not possible and suggests alternative methods like completing the square or using the quadratic formula. The discriminant is calculated to determine the nature of the solutions, revealing complex solutions. The quadratic formula is applied, and the complex solutions are simplified and interpreted.

What is the equation discussed in the video?

• x^2 + 6x + 10 = 0

• x^2 + 6x + 9 = 0

• x^2 + 6x + 15 = 0

• x^2 + 5x + 15 = 0

Tags

CCSS.HSA-REI.B.4B

Why can't the given quadratic equation be factored easily?

• The coefficients are too large

• No integers add up to 6 and multiply to 15

• The equation is not in standard form

• It can actually be factored easily

What method is suggested if one does not prefer completing the square?

• Graphical method

• Quadratic formula

• Trial and error

• Factoring

Tags

CCSS.HSA-REI.B.4B

What values are identified as a, b, and c in the quadratic formula?

• a = 0, b = 6, c = 15

• a = 15, b = 1, c = 6

• a = 6, b = 15, c = 1

• a = 1, b = 6, c = 15

Tags

CCSS.HSA-REI.B.4B

What is the coefficient 'b' in the discussed quadratic equation?

• 6

• 0

• 1

• 15

What is the value of the discriminant?

• 24

• -24

• 0

• -36

Tags

CCSS.HSA-REI.B.4B

What does a negative discriminant indicate about the roots of the equation?

• The equation has no roots

• There are no real roots, only complex ones

• There is one real root

• There are two real and distinct roots

Tags

CCSS.HSA-REI.B.4B

How is the square root of -24 simplified in the context of complex numbers?

• 2 sqrt(6)

• 4i sqrt(6)

• 4 sqrt(6)

• 2i sqrt(6)

Which of the following is a correct step in applying the quadratic formula?

• Add the discriminant to b

• Divide the discriminant by 2a

• Subtract 4ac from b^2

• Multiply b by 2a

Tags

CCSS.HSA-REI.B.4B

What is the simplified form of the solutions to the quadratic equation?

• -3 ± sqrt(6)

• -3 ± sqrt(6)i

• -3 ± i sqrt(6)

• -3 ± 2i sqrt(6)

Tags

CCSS.HSA-REI.B.4B

CCSS.HSN.CN.C.7