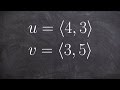
Determining the Angle Between Two Vectors

The video tutorial explains how to find the angle between two vectors using the cosine formula. It covers calculating the magnitudes of vectors U and V, finding their dot product, and using the inverse cosine function to determine the angle theta. The tutorial concludes with the final result of the angle calculation.

What formula is used to find the angle between two vectors?

• cos(theta) = (u + v) / (|u| + |v|)

• tan(theta) = (u * v) / (|u| * |v|)

• sin(theta) = (u * v) / (|u| * |v|)

• cos(theta) = (u * v) / (|u| * |v|)

What is the first step in finding the angle between two vectors?

• Draw the vectors on a graph

• Use the cosine inverse function

• Calculate the magnitudes of the vectors

• Calculate the dot product of the vectors

What is the magnitude of vector u if u = (4, 3)?

• 25

• 6

• 7

• 5

Tags

CCSS.HSN.VM.A.1

What is the result of 4 squared plus 3 squared?

• 16

• 12

• 25

• 9

Tags

CCSS.6.EE.A.1

What is the magnitude of vector v if v = (3, 5)?

• sqrt(34)

• sqrt(45)

• sqrt(25)

• 8

Tags

CCSS.HSN.VM.A.1

What is the dot product of vectors u = (4, 3) and v = (3, 5)?

• 34

• 32

• 27

• 25

How is the cosine of the angle theta calculated in vector mathematics?

• cos(theta) = dot product / (magnitude of u * magnitude of v)

• cos(theta) = dot product + (magnitude of u + magnitude of v)

• cos(theta) = dot product - (magnitude of u * magnitude of v)

• cos(theta) = dot product * (magnitude of u * magnitude of v)

Can the square root of 34 be simplified further in this context?

• Yes, to 5.83

• Yes, to 17

• Yes, to 2

• No

What tool did the teacher use to calculate the final angle?

• A ruler

• A protractor

• A calculator

• Graph paper

Tags

CCSS.4.MD.C.6

What is the value of theta when cos(theta) = 27 / (5 * sqrt(34))?

• 60 degrees

• 30 degrees

• 45 degrees

• 22.17 degrees

Tags

CCSS.HSF.TF.B.7