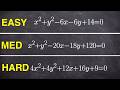
Understanding Circles: Center and Radius

The video tutorial explains how to find the center and radius of a circle by converting its equation from general form to standard form using the method of completing the square. It provides three examples, each with increasing complexity, demonstrating the process of grouping terms, finding the perfect square trinomial, and adjusting for coefficients. The tutorial emphasizes the importance of maintaining equality by performing operations on both sides of the equation and offers tips for factoring complex expressions.

What is the purpose of converting a circle's equation from general form to standard form?

• To simplify the equation for easier graphing

• To calculate the area of the circle

• To find the slope of the circle

• To determine the circle's diameter

Tags

CCSS.HSG.GPE.A.1

Which method is used to convert a circle's equation from general form to standard form?

• Substitution

• Using the quadratic formula

• Completing the square

• Factoring

Tags

CCSS.HSA-REI.B.4B

In the process of completing the square, what is the formula used to find the value that creates a perfect square trinomial?

• a + b = c

• b^2 - 4ac

• b/2 squared

• a^2 + b^2 = c^2

Tags

CCSS.HSA-REI.B.4B

When completing the square, why must you add the same value to both sides of the equation?

• To maintain the equation's balance

• To find the circle's radius

• To eliminate fractions

• To simplify the equation

Tags

CCSS.HSG.GPE.A.1

In the first example, what is the center of the circle after completing the square?

• (3, 3)

• (5, 5)

• (-3, -3)

• (0, 0)

Tags

CCSS.HSG.GPE.A.1

In the second example, what is the radius of the circle after completing the square?

• 9

• 10

• Square root of 5

• Square root of 61

Tags

CCSS.HSA-REI.B.4B

What is the first step when completing the square with a coefficient in front of the quadratic term?

• Add the coefficient to both sides

• Ignore the coefficient

• Factor out the coefficient

• Multiply the coefficient by the constant term

Tags

CCSS.HSG.GPE.A.1

In the complex example, what is the center of the circle after completing the square?

• (3/2, 2)

• (-3/2, -2)

• (0, 0)

• (2, 3)

Tags

CCSS.HSG.GPE.A.1

Why is it important to factor out the coefficient before completing the square?

• To make the equation easier to solve

• To ensure the equation is balanced

• To find the exact center of the circle

• To simplify the equation

Tags

CCSS.HSG.GPE.A.1

What is the radius of the circle in the complex example after completing the square?

• Square root of 16

• 2

• 4

• Square root of 9

Tags

CCSS.HSG.GPE.A.1