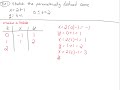
Understanding Parametric Equations

The video introduces parametric equations, contrasting them with rectangular equations. It explains how parametric equations incorporate a third variable, time, to provide more information about an object's path. The video details the process of graphing parametric equations by hand, including creating a table of values and plotting points. It also covers converting parametric equations to rectangular form and provides examples, including those involving trigonometric functions.

What is the main difference between parametric and rectangular equations?

• Rectangular equations cannot be graphed.

• Parametric equations are only used for circular paths.

• Rectangular equations are always linear.

• Parametric equations include a third variable, time.

In the example of the parabolic path, what does the parametric equation allow us to determine?

• The weight of the object.

• The position of the object at any given time.

• The speed of the object.

• The color of the object.

What is a plane curve in the context of parametric equations?

• A straight line on a graph.

• A curve that represents the path of an object over time.

• A graph that only uses the x-axis.

• A circle with a fixed radius.

What is the first step in graphing parametric equations by hand?

• Find the area under the curve.

• Calculate the derivative.

• Make a table of values for t, x, and y.

• Draw a straight line.

When converting parametric equations to rectangular form, what is a common first step?

• Solve one of the equations for t.

• Multiply both equations by 2.

• Divide the equations by x.

• Add the equations together.

Tags

CCSS.HSF-IF.C.7E

In the example of converting parametric to rectangular equations, what was the final rectangular equation?

• y = 2x + 3

• y = 1/2x + 3/2

• y = x^2 + 2

• y = 3x - 1

What is a key consideration when graphing parametric equations involving trigonometric functions?

• The angle must be 90 degrees.

• The sine and cosine functions are used.

• The graph must be a straight line.

• The equation must be quadratic.

Tags

CCSS.HSF-IF.C.7E

In the trigonometric parametric example, what was the range of the domain used?

• 0 to π/2

• 0 to 2π

• 0 to 1

• 0 to 3π/2

What is the rectangular equation derived from the trigonometric parametric example?

• x = 2y - 1

• x = y + 2

• x = 1/2y^2

• x = y^2

Why might it be difficult to solve for t directly in trigonometric parametric equations?

• The equations are not continuous.

• The equations do not involve time.

• The sine and cosine functions complicate the process.

• The equations are always linear.