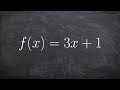
Understanding Inverse Functions

The video tutorial explains how to find the inverse of a function by interchanging input and output values. It covers the concept of inverse functions, graphical representation, and the algebraic process to find inverses. The tutorial concludes with an example, demonstrating the steps to solve for the inverse of a given function.

What is the primary concept behind finding the inverse of a function?

• Switching the input and output values

• Multiplying the function by -1

• Adding a constant to the function

• Dividing the function by its derivative

When finding the inverse of a function, what do you interchange?

• The exponents in the function

• The coefficients of the function

• The x and y values

• The constants in the function

Why is it often easier to use 'y' instead of 'f(x)' when finding an inverse?

• Because 'y' is always positive

• Because 'f(x)' is not a valid mathematical term

• Because it simplifies the algebraic process

• Because 'y' is a simpler letter

What is the first step in finding the inverse of a function algebraically?

• Divide by the coefficient of x

• Add 1 to both sides

• Change 'f(x)' to 'y'

• Multiply both sides by 2

In the example provided, what is the inverse of the function f(x) = 3x - 1?

• f inverse(x) = x - 1 / 3

• f inverse(x) = 3x + 1

• f inverse(x) = x + 1 / 3

• f inverse(x) = 1 - x / 3

What operation is performed after interchanging x and y to solve for y?

• Add 1 to both sides

• Subtract 1 from both sides

• Divide both sides by 3

• Multiply both sides by 3

What is the final step in finding the inverse of a function?

• Solve for y

• Multiply by the original function

• Verify the inverse by substitution

• Graph the function

What does the notation f inverse(x) represent?

• The derivative of the function

• The reciprocal of the function

• The inverse of the function

• The integral of the function

Why is it important to understand the concept of inverse functions?

• To graph functions more easily

• To solve complex equations

• To understand the relationship between variables

• To perform calculus operations

What is the significance of the negative one in the notation f inverse(x)?

• It indicates subtraction

• It denotes the inverse function

• It represents a negative slope

• It shows a decrease in value