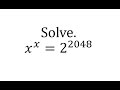
Understanding Exponent Properties and Solving Equations

The video tutorial explains how to solve the equation x^x = 2^2048 by using exponent properties. It begins with an introduction to the problem, followed by an explanation of the exponent property a^m^n = a^(m*n). The tutorial then applies this property to simplify the equation step-by-step, ultimately finding that x = 256. The process involves breaking down the powers and rewriting them until the base and exponent are the same, allowing for the solution to be determined.

What is the equation we are trying to solve in this tutorial?

• x^x = 2^1024

• x^x = 2^2048

• x^x = 4^512

• x^x = 16^256

Tags

CCSS.8.EE.A.1

Which property of exponents is used to solve the equation?

• a^m / a^n = a^(m-n)

• a^(m^n) = a^(m*n)

• a^m * a^n = a^(m+n)

• a^m + a^n = a^(m+n)

Tags

CCSS.6.EE.A.1

In the example given, how is 3^6 rewritten using the exponent property?

• 3^6 = 3^2 * 3^3

• 3^6 = 9^3

• 3^6 = 3^3 * 3^3

• 3^6 = 27^2

Tags

CCSS.8.EE.A.1

How is 2^2048 initially broken down using the exponent property?

• 2^2048 = 4^512

• 2^2048 = 2^512 * 2^512

• 2^2048 = 2^1024 * 2^1024

• 2^2048 = 4^1024

Tags

CCSS.6.EE.A.1

What is the next step after rewriting 4^1024 in the solution process?

• Rewrite as 8^512

• Rewrite as 4^512

• Rewrite as 2^512

• Rewrite as 16^512

What is the final expression before determining the value of x?

• 4^256

• 2^256

• 256^256

• 16^256

What is the value of x that solves the equation x^x = 2^2048?

• 512

• 1024

• 128

• 256