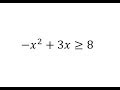
Quadratic Inequalities and Their Solutions

The video tutorial explains how to solve a quadratic inequality by first setting the equation to zero and attempting to solve it using factoring and the quadratic formula. The solutions are found to be complex, indicating no real solutions exist. The tutorial further tests values and verifies graphically that the inequality has no solution, concluding with a confirmation of this result.

What is the first step in solving a quadratic inequality?

• Set the right side to zero

• Multiply both sides by a variable

• Add a constant to both sides

• Divide both sides by a constant

Tags

CCSS.HSA-REI.B.4B

Why is factoring not possible for the equation in the video?

• The equation is already factored

• The equation is linear

• The equation has no constant term

• There are no factors of 8 that add to -3

Tags

CCSS.HSA-REI.B.4B

What method is used to solve the quadratic equation when factoring fails?

• Completing the square

• Graphing

• Quadratic formula

• Synthetic division

Tags

CCSS.HSA-REI.B.4B

CCSS.HSN.CN.C.7

What type of solutions are obtained from the quadratic formula in this case?

• Complex solutions

• Real solutions

• Integer solutions

• Rational solutions

What does the presence of complex solutions indicate about the inequality?

• There are infinitely many solutions

• There are no real solutions

• The inequality is always true

• The inequality is always false

Tags

CCSS.6.EE.B.5

What test value is used to check the inequality?

• x = 2

• x = 0

• x = -1

• x = 1

Tags

CCSS.6.EE.B.5

What conclusion is drawn from testing the inequality with x = 0?

• The inequality is true for negative numbers

• The inequality is true for positive numbers

• The inequality has no solution

• The inequality is true for all real numbers

How is the solution to the inequality verified graphically?

• By checking if the graph is parallel to the x-axis

• By checking if the graph is below the x-axis

• By checking if the graph intersects the x-axis

• By checking if the graph is above the x-axis

Tags

CCSS.8.F.A.1

CCSS.HSF.IF.B.5

What does it mean if the graph of the function is below the x-axis?

• The function values are negative

• The function values are zero

• The function values are positive

• The function values are undefined

What is the final conclusion about the quadratic inequality?

• It is always true

• It has a unique solution

• It has no solution

• It has multiple solutions