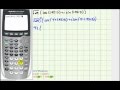
Complex Numbers and Their Properties

The video tutorial explains how to calculate the complex number -2 + 5i raised to the 4th power using De Moivre's Theorem. It begins by converting the complex number into polar form, graphing it on the complex plane, and determining the values of R and Theta. The tutorial then applies De Moivre's Theorem to raise the complex number to the 4th power, providing step-by-step calculations and using a calculator for verification. The final result is confirmed as 41 + 840i.

What is the initial complex number that needs to be raised to the 4th power?

• 5 - 3i

• 1 - 2i

• 3 + 4i

• -2 + 5i

Tags

CCSS.HSN.CN.B.4

Which theorem is used to raise the complex number to a power?

• Pythagorean Theorem

• De Moivre's Theorem

• Binomial Theorem

• Fermat's Last Theorem

What is the formula used to find the modulus of a complex number?

• R = √(X² + Y²)

• R = X + Y

• R = X² + Y²

• R = X - Y

In which quadrant is the angle theta located for the complex number -2 + 5i?

• Fourth Quadrant

• Third Quadrant

• Second Quadrant

• First Quadrant

Tags

CCSS.HSN.CN.B.4

What is the approximate value of theta in radians for the complex number -2 + 5i?

• 1.9513

• 3.1416

• 2.3562

• 0.7854

What is the result of raising the modulus to the 4th power?

• 29

• 841

• 58

• 145

Tags

CCSS.HSN.CN.B.4

What is the real part of the final result after applying De Moivre's Theorem?

• 100

• 41

• 29

• 58

Tags

CCSS.HSN.CN.B.4

What is the imaginary part of the final result after applying De Moivre's Theorem?

• 29i

• 58i

• 840i

• 100i

Tags

CCSS.HSN.CN.A.1

What mode should the calculator be in to verify the result?

• Degree Mode

• Scientific Mode

• Radian Mode

• Complex Mode

Tags

CCSS.HSN.CN.C.8

What is the final verified result of (-2 + 5i) raised to the 4th power?

• 58 + 29i

• 100 + 200i

• 29 + 58i

• 41 + 840i

Tags

CCSS.HSN.CN.C.8