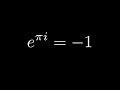
Understanding Euler's Identity

The video explains Euler's identity, e^(pi*i) = -1, and categorizes viewers based on their understanding. It reframes numbers as actions rather than counting, introducing concepts of adders and multipliers. The exponential function is explored, highlighting its role in transforming adders into multipliers. The video also delves into complex numbers, explaining their actions on the 2D plane, including sliding and rotating. The explanation aims to make the concept intuitive without requiring advanced math knowledge.

What are the three categories of viewers mentioned in the introduction?

• Those who have seen the equation in calculus but find it magical

• Those who are unclear about the terms

• Those who find the equation nonsensical

• Those who understand the equation completely

Tags

CCSS.HSN.CN.B.4

How should we think about numbers according to the new perspective introduced?

• As mere counting tools

• As actions that slide and stretch

• As complex equations

• As static points on a line

Tags

CCSS.HSN.CN.B.4

What is the primary goal of the function e^x?

• To calculate irrational numbers

• To simplify complex numbers

• To transform adders into multipliers

• To perform repeated multiplication

Tags

CCSS.HSF-IF.C.8B

What is the defining property of e^x?

• e^(x-y) equals e^x divided by e^y

• e^x equals x times e

• e^x equals x plus e

• e^(x+y) equals e^x times e^y

Tags

CCSS.HSN.CN.B.4

How are complex numbers represented in the 2D plane?

• As irrational numbers

• As adders and multipliers

• As static points only

• As simple lines

Tags

CCSS.HSN.CN.A.1

What action does the complex number 'i' perform as a multiplier?

• Slides the plane sideways

• Rotates the plane a quarter turn

• Stretches the plane

• Shrinks the plane

Tags

CCSS.HSN.CN.A.1

What does e^x do to points on the vertical line in the complex plane?

• Compresses them to a point

• Stretches them infinitely

• Maps them onto a circle

• Turns them into horizontal lines

Tags

CCSS.HSF.TF.A.4

What is the significance of the length of 2π in the context of e^x?

• It represents the diameter of a circle

• It is the area of a circle

• It is the radius of a circle

• It is the length needed to wrap around a circle

Tags

CCSS.HSN.CN.B.4

What does e^(pi*i) equal to?

• 1

• -1

• 0

• i

Tags

CCSS.HSN.CN.B.4

What is the natural way e^x behaves in the complex plane?

• It rotates lines by 180 degrees

• It compresses lines to points

• It wraps lines around circles

• It stretches lines infinitely

Tags

CCSS.HSN.CN.B.4