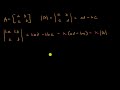
Determinants of Matrices Concepts
Interactive Video
•
Mathematics
•
9th - 12th Grade
•
Practice Problem
•
Hard
Lucas Foster
FREE Resource
Read more
5 questions
Show all answers
1.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the determinant of a 2x2 matrix with elements a, b, c, and d?
a * c - b * d
a * b + c * d
a * d - b * c
a + d - b - c
2.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
If you multiply the first row of a 2x2 matrix by a constant k, how does the determinant change?
It becomes k times the original determinant.
It becomes zero.
It remains the same.
It becomes k squared times the original determinant.
3.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What happens to the determinant if both rows of a 2x2 matrix are multiplied by a constant k?
It remains unchanged.
It becomes k squared times the original determinant.
It becomes zero.
It becomes k times the original determinant.
4.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the general formula for the determinant of an n by n matrix when multiplied by a constant k?
k cubed times the determinant of the matrix
k to the nth power times the determinant of the matrix
k squared times the determinant of the matrix
k times the determinant of the matrix
5.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What should you do to understand the determinant property for a 3x3 matrix?
Try adding a constant to each element.
Try multiplying the entire matrix by a constant.
Try multiplying only one row by a constant.
Try subtracting a constant from each element.
Access all questions and much more by creating a free account
Create resources
Host any resource
Get auto-graded reports
Continue with Google
Continue with Email
Continue with Microsoft
or continue with
%20(1).png)
Apple
Others
By signing up, you agree to our Terms of Service & Privacy Policy
Already have an account?
