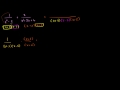
Understanding Rational Expressions and Common Denominators

The video tutorial explains how to add rational expressions by finding a common denominator. It begins with a simple example using fractions to illustrate the concept of the least common multiple. The tutorial then moves on to factor denominators of rational expressions and adjust numerators to match the common denominator. Finally, it demonstrates how to combine the expressions into a single rational expression.

Why is it necessary to find a common denominator when adding rational expressions?

• To ensure the numerators are equal

• To convert them into improper fractions

• To simplify the expressions

• To make the denominators identical for addition

Tags

CCSS.HSA.APR.D.7

What is the first step in adding rational expressions with different denominators?

• Add the numerators directly

• Find a common denominator

• Multiply the expressions

• Subtract the smaller denominator from the larger one

What is the least common multiple of 1/4 and 1/6?

• 18

• 6

• 12

• 24

Tags

CCSS.HSA.APR.C.4

How do you factor the expression x^2 - 9?

• (x + 3)(x - 3)

• (x - 3)(x - 3)

• (x + 3)(x + 3)

• (x + 2)(x - 2)

Tags

CCSS.HSA.APR.D.7

What is the least common denominator of the expressions 1/(x^2 - 9) and 2/(x^2 + 5x + 6)?

• (x + 3)(x - 3)(x + 2)

• (x + 3)(x + 2)

• (x - 3)(x + 2)

• (x + 3)(x - 3)

Tags

CCSS.HSA.APR.D.7

What additional factor is needed in the denominator of 1/(x^2 - 9) to match the least common denominator?

• x + 2

• x - 2

• x + 3

• x - 3

Tags

CCSS.HSA.APR.D.6

What is the purpose of multiplying the numerator and denominator by the same expression?

• To simplify the expression

• To make the expression more complex

• To change the value of the expression

• To maintain the value while changing the form

Tags

CCSS.6.EE.A.3

What is the result of multiplying 2 by (x - 3)?

• 2x - 6

• 2x + 6

• 2x + 3

• 2x - 3

Tags

CCSS.HSA.APR.D.7

What is the simplified form of the expression 3x - 4 over the common denominator?

• 3x - 4

• 3x + 4

• 3x - 6

• 3x + 6

Tags

CCSS.HSA.APR.D.7

What is the result of adding the expressions 1/(x^2 - 9) and 2/(x^2 + 5x + 6) after finding a common denominator?

• 3x - 6 over (x + 3)(x - 3)(x + 2)

• 3x + 6 over (x + 3)(x - 3)(x + 2)

• 3x + 4 over (x + 3)(x - 3)(x + 2)

• 3x - 4 over (x + 3)(x - 3)(x + 2)

Tags

CCSS.HSA.APR.D.7