Understanding Quadratic Functions and Graphing Calculators

The video tutorial explains how to use a graphing calculator to model the trajectory of a golf ball using quadratic regression. It starts with introducing the problem and data points, followed by instructions on using the calculator to input data and set up the graph. The tutorial then demonstrates performing quadratic regression to fit the data and analyzes the results, comparing them with theoretical values in a vacuum.

What is the initial speed of the golf ball when it is hit?

• 40 meters per second

• 30 meters per second

• 50 meters per second

• 60 meters per second

Which key do you press first to start entering data into the graphing calculator?

• Stat

• Mode

• Calc

• Graph

What is the purpose of setting the x and y ranges on the graphing calculator?

• To increase the speed of calculations

• To ensure all data points are visible

• To save battery life

• To change the color of the graph

What type of regression is used to fit the data points in this tutorial?

• Quadratic regression

• Linear regression

• Exponential regression

• Logarithmic regression

Which of the following is NOT a type of regression mentioned in the tutorial?

• Linear regression

• Quadratic regression

• Cubic regression

• Logarithmic regression

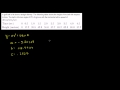
What is the value of the coefficient 'a' in the quadratic equation obtained from the regression?

• 35.99

• -5.2

• 0.29

• -4.9

How does air resistance affect the quadratic function compared to the theoretical model?

• It makes the function exponential.

• It causes the coefficients to differ.

• It has no effect.

• It makes the function linear.

What is the significance of the coefficient 'c' in the quadratic equation?

• It represents the angle of projection.

• It represents the time of flight.

• It represents the maximum height of the ball.

• It represents the initial height of the ball.

What is the predicted height of the golf ball at 5.2 seconds using the quadratic function?

• 46.83 meters

• 50.00 meters

• 55.00 meters

• 60.00 meters

What is the main advantage of using a graphing calculator for this analysis?

• It automatically adjusts for air resistance.

• It eliminates the need for data input.

• It simplifies complex calculations.

• It provides exact theoretical values.