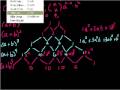
Understanding the Binomial Theorem and Pascal's Triangle

The video tutorial explains the binomial theorem and its application in expanding expressions like (a+b)^n. It highlights the tedious nature of manual expansion and introduces the binomial theorem as a solution. The tutorial then demonstrates using Pascal's Triangle to simplify the process of finding binomial coefficients. Finally, it presents an even faster method for calculating these coefficients, allowing for quick expansion of expressions to higher powers.

Why is it tedious to expand (a + b)^n for larger values of n?

• Because it requires solving differential equations.

• Because it involves complex calculus.

• Because it involves repetitive multiplication.

• Because it needs advanced algebraic techniques.

What is the role of 'n choose k' in the binomial theorem?

• It determines the number of terms in the expansion.

• It represents the coefficients in the expansion.

• It calculates the power of b in each term.

• It calculates the power of a in each term.

How does Pascal's Triangle help in binomial expansion?

• It gives the coefficients for each term in the expansion.

• It simplifies the multiplication process.

• It helps in calculating the powers of a and b.

• It provides a visual representation of the expansion.

What is the pattern observed in Pascal's Triangle?

• The numbers are random.

• The numbers are symmetric.

• The numbers decrease linearly.

• The numbers form a geometric sequence.

What is a limitation of using Pascal's Triangle for large powers?

• It becomes too complex to draw.

• It requires advanced mathematical knowledge.

• It takes too much time to compute.

• It is not accurate for large numbers.

What is the first step in the faster method for binomial expansion?

• Calculate the sum of coefficients.

• Write down the number of terms.

• Draw Pascal's Triangle.

• Multiply all terms together.

How do you determine the coefficient of the second term in the faster method?

• Multiply the first term's coefficient by its exponent.

• Divide the first term's coefficient by its exponent.

• Add the first term's coefficient to its exponent.

• Subtract the first term's coefficient from its exponent.

What is the significance of the middle term in the binomial expansion?

• It has the smallest coefficient.

• It is the same as the last term.

• It has the largest coefficient.

• It is the same as the first term.

Why is the faster method advantageous for large powers?

• It uses fewer mathematical operations.

• It is quicker and less prone to errors.

• It is more accurate.

• It requires less memory.

What is the final step in the faster method for binomial expansion?

• Write out the full expanded expression.

• Check the symmetry of coefficients.

• Verify the result using calculus.

• Recalculate using Pascal's Triangle.