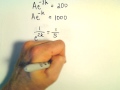
Population Growth and Modeling Concepts

The video tutorial explains how to solve an exponential growth problem related to bacterial population using differential equations. It starts by setting up the problem with known data points and defining the population equation. The tutorial then derives the growth rate using natural logarithms and simplifies the equation for easier prediction. It calculates the initial population and uses the model to predict the population size one day later, concluding with an expected population of about 5,000 bacteria.

What is the initial condition of the bacterial population 3 days ago?

• 1,000 bacteria

• 500 bacteria

• 200 bacteria

• 100 bacteria

Which equation represents the population growth model?

• P(t) = a + kt

• P(t) = a * e^(kt)

• P(t) = a * kt

• P(t) = a / e^(kt)

What does the variable 't' represent in the population model?

• Total population

• Growth rate

• Temperature

• Time in days

How do we determine the growth rate 'k' in the model?

• By subtracting the initial population from the final population

• By dividing the initial population by the final population

• By taking the natural logarithm of the ratio of populations at different times

• By multiplying the initial population by the final population

What is the simplified expression for the population growth after finding 'k'?

• P(t) = a * 5^t

• P(t) = a * 2^t

• P(t) = a * e^(5t)

• P(t) = a * (5/2)^t

What mathematical operation is used to solve for 'k'?

• Natural logarithm

• Addition

• Subtraction

• Multiplication

How is the initial population 'a' determined?

• By using the population value at t = 0

• By using the final population value

• By solving the equation with known population values

• By guessing based on the growth rate

What is the initial population value 'a' in the model?

• Square root of 5 times 1,000

• 5,000

• 5 times 1,000

• 1,000

Why is it acceptable that the initial population 'a' is not a whole number?

• Because it is an approximation

• Because it is a constant

• Because it is a variable

• Because it is a whole number

What is the expected population one day later?

• 10,000 bacteria

• 5,000 bacteria

• 3,000 bacteria

• 2,000 bacteria