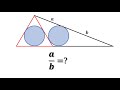
Properties of Inscribed Circles and Triangles

The video tutorial explores two triangles, ABC and BDC, with inscribed circles of the same radius. It explains the properties of inscribed circles, congruent triangles, and relationships between sides. The tutorial derives area and perimeter relationships and discusses equilateral triangle properties. It concludes with final calculations to find the ratio of sides a and b.

What is the main task described in the problem involving triangles ABC and BDC?

• To determine the length of side BC

• To find the ratio of segments a and b

• To calculate the perimeter of triangle BDC

• To find the area of triangle ABC

What is a key property of an inscribed circle in a triangle?

• It is always equilateral

• It is always larger than the triangle

• It is tangent to all three sides of the triangle

• It is always centered at the centroid of the triangle

What is the relationship between the radius of an inscribed circle and the tangent line?

• The radius is equal to the tangent line

• The radius bisects the tangent line

• The radius is perpendicular to the tangent line

• The radius is parallel to the tangent line

How are the triangles FOD and EOD related?

• They are similar

• They are scalene

• They are congruent

• They are isosceles

What formula is derived for the area of a triangle using the inscribed circle?

• Area = radius × (a + b + c)

• Area = radius × (a + b + c) / 2

• Area = radius × perimeter

• Area = radius × (a + b + c) / 3

In an equilateral triangle, where is the point of tangency of the inscribed circle located?

• At the midpoint of each side

• At the vertex of the triangle

• At the centroid of the triangle

• At the orthocenter of the triangle

What type of triangle is formed by the altitude in triangle ABC?

• 45-45-90 triangle

• 30-60-90 triangle

• Equilateral triangle

• Isosceles triangle

What is the relationship between the angles in the quadrilateral GOCF?

• The angles are all equal

• The angles are split into two congruent parts

• All angles are 60 degrees

• All angles are 90 degrees

What is the final ratio of a over b as determined in the problem?

• 1:2

• 2:3

• 5:9

• 3:4

How are the triangles GCO and FCO related?

• They are congruent

• They are similar

• They are isosceles

• They are scalene