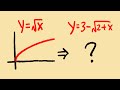
Graph Transformations and Function Analysis

The video tutorial explains how to graph a function using transformations. It starts with the function f(x) = 3 - √(2 + x) and breaks it down into components. The tutorial covers shifting the graph two units to the left, flipping it upside down about the x-axis, and shifting it vertically upwards by three units. The final graph is analyzed to determine its domain and range, which are from -2 to infinity and from negative infinity to 3, respectively.

What is the basic shape of the graph of the square root function?

• A complete parabola

• A sideways parabola without the bottom half

• A straight line

• A circle

What happens to the graph when 2 is added directly to the x-value?

• The graph shifts two units to the right

• The graph shifts two units to the left

• The graph shifts two units upwards

• The graph shifts two units downwards

What is the starting point of the graph after the horizontal shift?

• x = 0

• x = -2

• x = 2

• x = -3

How does a negative sign in front of the square root affect the graph?

• It stretches the graph vertically

• It flips the graph upside down

• It shifts the graph to the left

• It shifts the graph to the right

After the vertical flip, where does the graph start?

• At x = 2

• At x = -2

• At x = 3

• At the origin

What is the effect of adding 3 to the function?

• The graph shifts three units to the left

• The graph shifts three units to the right

• The graph shifts three units upwards

• The graph shifts three units downwards

Which transformation is applied last to the function?

• Vertical shift

• Horizontal flip

• Vertical flip

• Horizontal shift

What is the domain of the function f(x) = 3 - √(2 + x)?

• (-∞, 2]

• [-2, ∞)

• (-∞, -2]

• (-2, ∞)

What is the range of the function f(x) = 3 - √(2 + x)?

• (-∞, 3]

• [3, -∞)

• [3, ∞)

• (-∞, 3)

What is the highest point on the graph after all transformations?

• y = 3

• y = -2

• y = 2

• y = 0