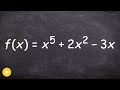
Polynomial Degree and End Behavior
Interactive Video
•
Mathematics
•
9th - 10th Grade
•
Hard
Patricia Brown
FREE Resource
Read more
10 questions
Show all answers
1.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the first step in determining the end behavior of a polynomial?
Calculate the derivative of the polynomial
Arrange the polynomial in descending order of power
Identify the roots of the polynomial
Find the constant term
2.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the leading coefficient of a polynomial?
The sum of all coefficients
The coefficient of the term with the highest power
The constant term of the polynomial
The coefficient of the term with the lowest power
3.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
How can you determine if a polynomial's degree is even or odd?
By counting the number of terms in the polynomial
By finding the sum of all coefficients
By looking at the highest power of the polynomial
By checking if the polynomial has a constant term
4.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What does a graph with an odd degree and a positive leading coefficient generally look like?
It rises to the left and falls to the right
It is a vertical line
It falls to the left and rises to the right
It is a horizontal line
5.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What does the end behavior of a polynomial tell us?
The roots of the polynomial
The y-intercept of the graph
The behavior of the graph as x approaches infinity
The exact shape of the graph
6.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
As x approaches negative infinity, what happens to the graph of a polynomial with an odd degree and positive leading coefficient?
The graph rises
The graph falls
The graph remains constant
The graph oscillates
7.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
As x approaches positive infinity, what happens to the graph of a polynomial with an odd degree and positive leading coefficient?
The graph oscillates
The graph falls
The graph remains constant
The graph rises
Create a free account and access millions of resources
Similar Resources on Wayground

11 questions
End Behavior of Polynomials
Interactive video
•
9th - 10th Grade

10 questions
Analyzing Polynomial Functions Concepts
Interactive video
•
9th - 10th Grade

9 questions
Cubic and Polynomial Functions Concepts
Interactive video
•
9th - 10th Grade

11 questions
Polynomial End Behavior and Characteristics
Interactive video
•
9th - 10th Grade

11 questions
Understanding Polynomial Functions and Graphs
Interactive video
•
9th - 10th Grade

8 questions
Determining End Behavior of Graphs by Analyzing Equations
Interactive video
•
9th - 10th Grade

11 questions
Comparing Polynomial Functions Behavior
Interactive video
•
9th - 10th Grade

6 questions
Finding the end behavior when given an equation
Interactive video
•
9th - 10th Grade
Popular Resources on Wayground

55 questions
CHS Student Handbook 25-26
Quiz
•
9th Grade

18 questions
Writing Launch Day 1
Lesson
•
3rd Grade

10 questions
Chaffey
Quiz
•
9th - 12th Grade

15 questions
PRIDE
Quiz
•
6th - 8th Grade

40 questions
Algebra Review Topics
Quiz
•
9th - 12th Grade

22 questions
6-8 Digital Citizenship Review
Quiz
•
6th - 8th Grade

10 questions
Nouns, nouns, nouns
Quiz
•
3rd Grade

10 questions
Lab Safety Procedures and Guidelines
Interactive video
•
6th - 10th Grade
Discover more resources for Mathematics

40 questions
Algebra Review Topics
Quiz
•
9th - 12th Grade

14 questions
Points, Lines, Planes
Quiz
•
9th Grade

15 questions
Adding and Subtracting Polynomials
Quiz
•
9th Grade

20 questions
1.1 (a) Classifying Polynomials
Quiz
•
9th Grade

12 questions
Classifying Polys - 1.1
Quiz
•
10th - 12th Grade

20 questions
Function or Not? Domain and Range
Quiz
•
9th - 12th Grade

20 questions
Order of Operations
Quiz
•
9th Grade

19 questions
Constructions Review SKG
Quiz
•
10th Grade