Linear Transformations in Vector Spaces
Interactive Video
•
Mathematics
•
9th - 12th Grade
•
Hard
Patricia Brown
FREE Resource
Read more
10 questions
Show all answers
1.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the primary focus of linear transformations in vector spaces?
To transform vectors within or between vector spaces
To create new vector spaces
To change the dimension of vectors
To map vectors to scalars
2.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
How can a linear transformation be denoted when mapping from vector space V to W?
L: W → W
L: W → V
L: V → W
L: V → V
3.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
Which property must a linear transformation satisfy when dealing with scalar multiplication?
Scalar multiplication is not allowed
The transformation of a scalar is zero
Scalar multiplication and transformation commute
The transformation of a scalar is a vector
4.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the result of transforming the sum of two vectors in a linear transformation?
A scalar value
The sum of the transformations of each vector
The difference of the transformations of each vector
A matrix
5.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the significance of verifying the properties of linear transformations?
To demonstrate they are matrices
To prove they are scalar
To confirm they are linear
To ensure they are non-linear
6.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What does the commutativity of operations in linear transformations imply?
Only scalar multiplication is commutative
Operations must be performed in a specific order
Order of operations does not matter
Only vector addition is commutative
7.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
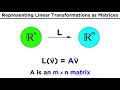
How can linear transformations from Rn to Rm be represented?
As a vector
As a polynomial
As a matrix
As a scalar
Create a free account and access millions of resources
Similar Resources on Wayground

11 questions
Understanding Linear Dependence of Vectors
Interactive video
•
9th - 12th Grade

11 questions
Understanding Linear Transformations and Matrix Multiplication
Interactive video
•
10th - 12th Grade

11 questions
Understanding Vector Coordinates and Basis Transformation
Interactive video
•
9th - 12th Grade

11 questions
Linear Transformations and Their Compositions
Interactive video
•
10th - 12th Grade

11 questions
Understanding Linear Transformations and Eigenvectors
Interactive video
•
9th - 12th Grade

11 questions
Matrix Transformations and Multiplication Concepts
Interactive video
•
10th - 12th Grade

11 questions
Understanding Systems of Equations and Matrices
Interactive video
•
9th - 12th Grade

11 questions
Linear Combinations and Vector Operations
Interactive video
•
9th - 12th Grade
Popular Resources on Wayground

10 questions
Lab Safety Procedures and Guidelines
Interactive video
•
6th - 10th Grade

10 questions
Nouns, nouns, nouns
Quiz
•
3rd Grade

10 questions
Appointment Passes Review
Quiz
•
6th - 8th Grade

25 questions
Multiplication Facts
Quiz
•
5th Grade

11 questions
All about me
Quiz
•
Professional Development

22 questions
Adding Integers
Quiz
•
6th Grade

15 questions
Subtracting Integers
Quiz
•
7th Grade

20 questions
Grammar Review
Quiz
•
6th - 9th Grade
Discover more resources for Mathematics

20 questions
Order of Operations
Quiz
•
9th Grade

13 questions
8th - Unit 1 Lesson 3
Quiz
•
9th - 12th Grade

15 questions
Two Step Equations
Quiz
•
9th Grade

16 questions
Segment Addition Postulate
Quiz
•
10th Grade

12 questions
Absolute Value Equations
Quiz
•
9th Grade

7 questions
EAHS PBIS Lesson- Bus
Lesson
•
9th - 12th Grade

21 questions
SOLVING TWO STEP EQUATIONS
Quiz
•
9th Grade

15 questions
Combine Like Terms and Distributive Property
Quiz
•
8th - 9th Grade